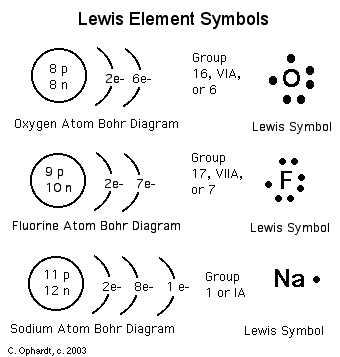
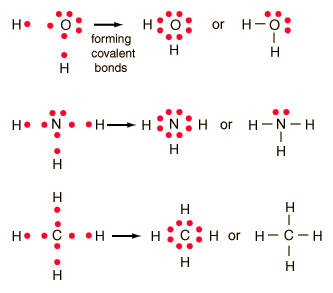
Lewis Symbols or Diagrams
Chemical identity is determined by the number of
protons within the nucleus of an atom, atomic mass is determined by the
number of protons and neutrons within the nucleus and chemical bonding
is largely determined by the number of outermost or valence electrons within
the atom. Thus, electrons in completely filled energy levels are
mostly ignored when considering chemical properties. Simplified Bohr
diagrams which only consider electrons in outer energy levels are called
Lewis Symbols. A Lewis Symbol consists of the element symbol surrounded
by "dots" to represent the number of electrons in the outer energy level
as represented by a Bohr Diagram. In a Lewis symbol, the inner closed
shells of electrons can be considered as included in chemical symbol for
the element, and the outer shell or valence electrons are represented by
dots. The dots are placed in four groups of one or two electrons
each, with 8 electrons representing a closed shell or noble gas configuration.
Lewis diagrams are useful for visualizing both ionic and covalent bonds.
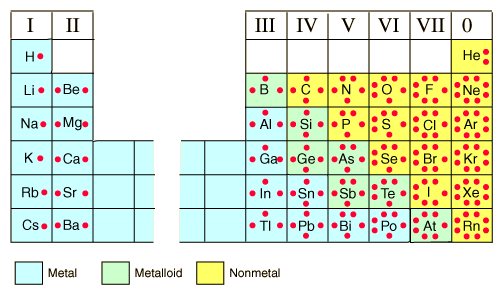
The number of valence electrons for an atom is often, but not always, determined
from the position of that element on the periodic table.
Consider the following examples:
Thus, we would see that each family has the same
Lewis Symbols configuration and each element in a period has one more electron/dot
than the previous element for representative elements.
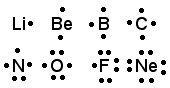
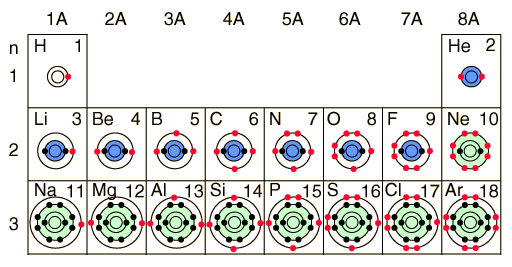
As you can see this correlates with the Bohr-Rutherford
diagrams and electronic configurations as well.
However, we must notice that the ground state of
some of the elements (Be, B, C) is not the same as the bonding state.
In other words, the element in free space in it's minimum energy configuration
(ground state) is not necessarily the same as the element in a molecule.
To reconfigure an atom into its 'normal valence' state, we can split the
non-bonding pair (lone pair) of electrons into two unpaired electrons.
In the case of Be, we split the two 2s electrons into two unpaired electrons
(into orbitals not necessarily called 2s and 2p but we'll get to that later).
Similarly, we can expand the valence of B and C by splitting their lone
pairs into single electrons. In each of these cases, we increase
the "valence" by 2 for each lone pair we split up. We can do this because
there are a maximum of 4 orbitals at the n=2 quantum level into which we
can put electrons with minimal expense energy-wise. If we tried to
split the lone pair on Nitrogen into two unpaired electrons we would run
into the limit of the number of orbitals. N, has only 4 orbitals
(places) to hold electrons. The normal ground state of N already
has at least 1 electron in each of the four orbitals. If we tried
splitting the lone pair we would have no place to put the extra electron
without moving it to an n=3 orbital. That would cost too much energy.
Thus, we represent the ground state in a unique
manner to convey the precise orbital placement of valence electrons.
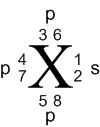
Note that the actual order beyond the s orbital is
arbitrary other than electrons must be placed singly before pairing.
So the order of 3, 4 and 5 does not matter as long as 6,7 and 8 are not
filled before 5. Once at atom enters into bonding, these positions
are not followed as hybridization and promotions have priority not to mention
that atoms re-orientate themselves to align properly for bonding.
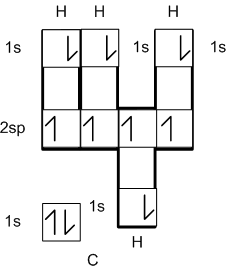
Lewis diagrams are much more convenient to demonstrate
bonding than electronic configurations or orbital box diagrams. Consider
the orbital box diagrams for the following bonded atoms:
CH4 (more on this configuration later).
O2
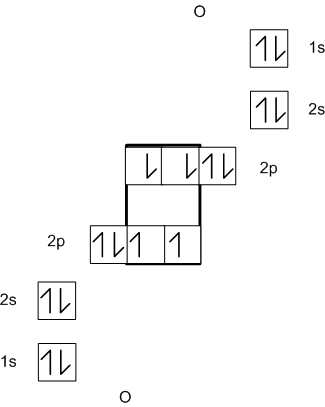
As you can see these, diagrams convey a lot of information,
but are rather cumbersome and most of the electrons are not involved in
the bonding. Lewis diagrams simplify and focus attention of the relevant
atomic interactions. There are two types of bonds to consider, one
involving electron transfer (loss and gain) and the other involving a compromise
or sharing of electrons.
Ionic Bonding
Typically this involves that bonding of a metal with
a non-metal atom. Since metals have very low attraction for their
outer electrons while non-metals have such a high affinity for outer electrons,
the non-metals successfully steal outer electrons from metal atoms.
Thus, there is a transfer of electrons from one atom to another resulting
in the formation of positive and negative charges. The conditions
for bonds are that the total charge is zero and that each atom must have
a noble gas electron configuration. Consider some examples:
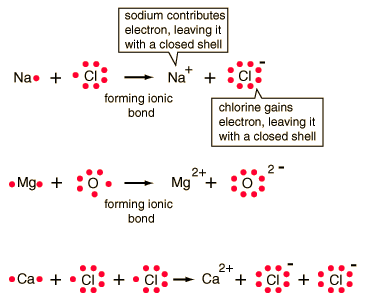
In order to illustrate the actual bonding that took
place, electron transfers are usually conveyed.
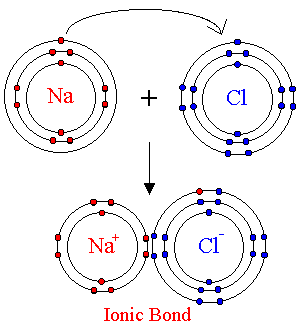
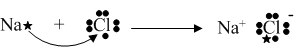
Likewise, other bonds could be shown:
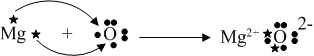
The only force acting within this chemical bond is
the force of attraction between charged particles. This attraction
lacks definitive direction in that it acts in every direction. As
a result ionic solids tend to be crystals of numerous ions and when placed
in water, the ions easily attract to the polar water molecules and the
solid breaks apart or dissolves. Notice that for each ion, the result
is a full, stable octet, that is the atoms have not obtained the electronic
configuration of a noble gas. Typically this means 8 outer electrons,
but actually it means full outer orbitals.
Covalent Bonding
In the idealized covalent bond, two atoms share a
pair of electrons, closing the shell for each of them. The atoms
share a pair of electrons, and that pair is referred to as a bonding pair.
The pairs of electrons which do not participate in the bond have traditionally
been called "lone pairs". A single bond can be represented by the
two dots of the bonding pair, or by a single line which represents that
pair. The single line representation for a bond is commonly used
in drawing Lewis structures for molecules.
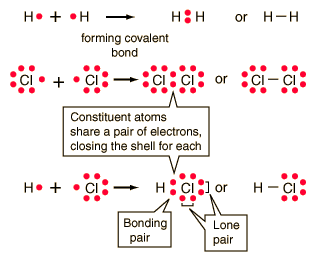
Sometimes it is easier to visualize how the bonding
took place if the bonding pairs of electrons are joined.

The actual chemical bond formed is a permanent connection
resulting in a new particle. The shape of the molecule is determined
by the number of valence electrons present (more on that later).
The actual bond itself is really due to an overlap of
the valence electrons resulting in a new orbital configuration.

The relative strength of the nucleus of each atom
involved in the bonding determines how far apart the atoms remain once
the overlap has taken place. This distance is referred to as the
bond length.
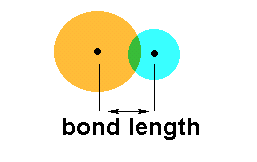
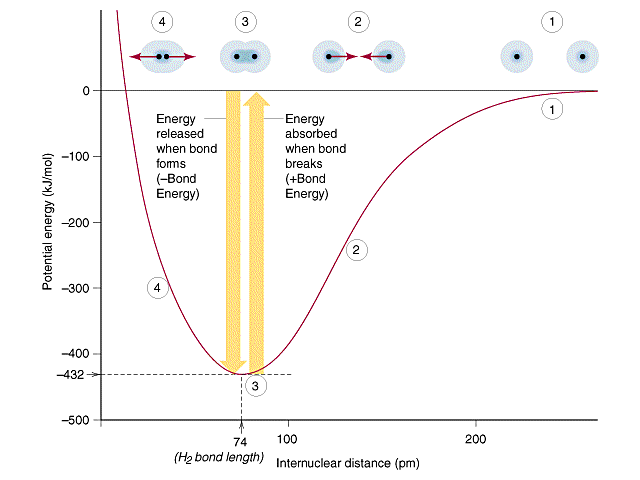
The formation of the bond is determined by the interplay
of the attractive forces expressed between the nucleus of one atom and
the outer electrons of the other. However, as the atoms approach
one another, the forces of repulsion between the outer electrons and nuclei
of each atom start to force the atoms apart. When the force of repulsion
equals the force of attraction, the bond forms.
Or a simpler version would be:
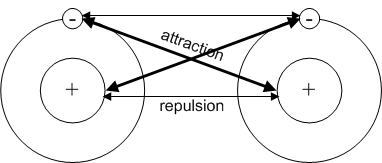
Lewis symbols and Lewis diagrams can be used to describe
multiple bonds,.
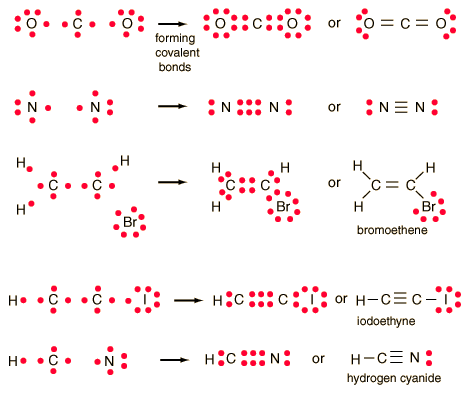
Electrons are typically not shared equally within
a covalent bond as one atom may have a stronger hold on the shared pair
of electrons than the other atom causing the shared pair of electrons to
orbit closer to that stronger atom for a larger percentage of time.
Electronegativity is a measure of the tendency of an atom to attract a
bonding pair of electrons. The Pauling scale is the most commonly
used. Fluorine (the most electronegative element) is assigned a value of
4.0, and values range down to cesium and francium which are the least electronegative
at 0.7. The most electronegative element is fluorine. If you
remember that fact, everything becomes easy, because electronegativity
must always increase towards fluorine in the Periodic Table. This
simplification ignores the noble gases. Historically this is because they
were believed not to form bonds - and if they don't form bonds, they can't
have an electronegativity value. Even now that we know that some
of them do form bonds, data sources still don't quote electronegativity
values for them.
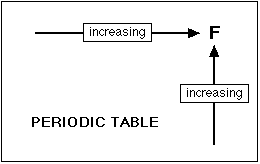
The attraction that a bonding pair of electrons feels
for a particular nucleus depends on the number of protons in the nucleus;
the distance from the nucleus; and the amount of screening by inner electrons.
As you go across a period the electronegativity increases because the number
of charges on the nucleus increases. That attracts the bonding pair of
electrons more strongly. As you go down a group, electronegativity
decreases because the bonding pair of electrons is increasingly distant
from the attraction of the nucleus.
Consider a bond between two atoms, A and B.
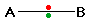
Each atom may be forming other bonds as well as the
one shown - but these are irrelevant to the argument. If the atoms
are equally electronegative, both have the same tendency to attract the
bonding pair of electrons, and so it will be found on average half way
between the two atoms. In actuality, the shared pair of electrons
move back and forth to some degree, but on average they are equally distributed.
To get a bond like this, A and B would usually have to be the same atom.
You will find this sort of bond in, for example, H2 or Cl2
molecules. This sort of bond could be thought of as being a "pure"
covalent bond - where the electrons are shared evenly between the two atoms.
Consider now, what happens if B is slightly more
electronegative than A. B will attract the electron pair rather more
than A does.
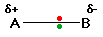
That means that the B end of the bond has more than
its fair share of electron density and so becomes slightly negative.
At the same time, the A end (rather short of electrons) becomes slightly
positive. In the diagram, "" (read as "delta") means "slightly" - so +
means "slightly positive".
The implication of all this is that there is no clear-cut
division between covalent and ionic bonds. I n a pure covalent bond, the
electrons are held on average exactly half way between the atoms.
In a polar bond, the electrons have been dragged slightly towards one end.
How far does this dragging have to go before the bond counts as ionic?
There is no real answer to that. You normally think of sodium chloride
as being a typically ionic solid, but even here the sodium hasn't completely
lost control of its electron. Because of the properties of sodium
chloride, however, we tend to count it as if it were purely ionic.
For atoms that share electrons equally,
there is no percent ionic character to the bond. In other words,
the percent ionic character is 0. This means that the shared pair
of electrons is not distributed closer to one atom on average. Atoms
that share an electron pair unequally will have a certain degree of ionic
character to its bond. To determine the percent ionic character of
a bond, you will need to know the electronegativities of the atoms involved.
Then calculate the difference in the electronegativities. This difference
is then translated to a percent ionic character by using a chart or graph
as a reference. For example, an electronegativity difference of 1.7
is said to be 51% ionic. Thus any difference in electronegativity
between two atoms exceeding 1.7 is considered enough ionic character to
indicate that one of the atoms is likely to hold the shared pair more often
than 50% of the time making this bond ionic greater than n50% of the time.
Some texts state 2.0 is the critical division between polar covalent and
ionic. This inconsistency should be understandable since numerous
bonds have electronegativity differences greater than 1.7 yet remain polar
instead of ionic due to other factors. The key factor is that this
scale represents the likelihood of acting ionically, not that actuality.
It is a predictive scale only. Obviously bonds with electronegativity
differences around 1.5 to 2.0 are going to sway back and forth from ionic
to polar covalent.
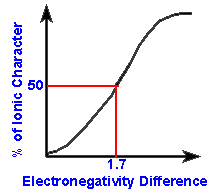
When the electronegativity difference is only 0.4,
the bond is only 4% ionic in character which means that there is only a
4% chance that the stronger atom will have the electrons closer to itself
than the other atom on average. Worded another way, 4% of the time,
the electrons are not equally distributed. Many texts state that
an electronegativity difference of 0 between atoms is the only pure covalent
bond. However, common sense would indicate that this is a gross assumption.
Many pure covalent bonds exist that have slight ionic character so numerous
sources identify any electronegativity under 0.4 as being pure covalent
because there is still a 96% chance of the electrons being shared equally.
In science 95% is considered an excellent confidence level. That
is, this is the mark that someone can be sure is essentially the same as
100% since chance will vary results slightly. Thus polar covalent
sharing of electrons is considered when the electronegativity difference
exceeds 0.4 and is under 1.7.
Intermolecular Bonding
Intramolecular forces of attraction act within a
compound or molecule to hold that molecule together. These forces
of attraction result in the typical bonds identified in chemistry: ionic,
covalent and polar covalent. It has been found that compounds and
molecules exist more readily as solids and liquids, than as gases indicating
that there must be a force of attraction between the particles. These
intermolecular forces of attraction account for a considerably array of
chemical and physical properties of these substances. There are two types
of intermolecular forces of attraction.
1. Ionic Forces of Attraction
In ionic compounds, the ions do not direct their
force of attraction between each other, but rather attract other ions in
all directions. For example Na+ is actually surrounded
by six chloride ions. Each chloride ion is likewise surrounded by
six sodium ions. Due to this strong intermolecular bond, ionic solids
have the following properties which all become more pronounced as the ionic
bond becomes stronger and/or the ions involved become smaller in size.
-
They have a high melting point since it is very difficult to pull one atom
away from another.
-
Solid ionic compounds do not conduct electricity since there are no free
ions to pass along electrons.
-
Liquid ionic compounds conduct electricity because the ions are attracted
to polar water which then separates and frees the ions from the lattice
collective.
-
Solid ionic compounds are typically odourless since the numerous attractions
prevent any ions from leaving the lattice collective.
-
Solid ionic compounds tend to fracture when struck since it takes considerable
force to separate ions from the lattice structure. to conduct electricity.
To show electrical conductivity, the ions in the mixture would need to
be free to move. Without dissolving in water, the ions are still fixed
in their crystal lattice positions.
2. Van der Waals Forces of Attraction
These forces of attraction are typically only 1%
of the strength of a covalent bond, but they can range from 0.001-15% of
the strength of a covalent bond. Individually they are weak,
but because they usually so numerous, they are collectively strong.
Water is the only substance we routinely encounter as a
solid, a liquid, and a gas. At low temperatures, it is a solid in which
the individual molecules are locked into a rigid structure. As we
raise the temperature, the average kinetic energy of the molecules increases,
which increases the rate at which these molecules move. The intramolecular
bonds that hold the atoms in H2O molecules together are almost
25 times as strong as the intermolecular bonds between water molecules.
(It takes 464 kJ/mol to break the H--O bonds within a water molecule and
only 19 kJ/mol to break the bonds between water molecules.)
All motion disrupt the bonds between water molecules.
As the system becomes warmer, the thermal energy of the water molecules
eventually becomes too large to allow these molecules to be locked into
the rigid structure of ice. At this point, the solid melts to form
a liquid in which intermolecular bonds are constantly broken and reformed
as the molecules move through the liquid. Eventually, the thermal
energy of the water molecules becomes so large that they move too rapidly
to form intermolecular bonds and the liquid boils to form a gas in which
each particle moves more or less randomly through space. The difference
between solids and liquids, or liquids and gases, is therefore based on
a competition between the strength of intermolecular bonds and the thermal
energy of the system. At a given temperature, substances that contain
strong intermolecular bonds are more likely to be solids. For a given
intermolecular bond strength, the higher the temperature, the more likely
the substance will be a gas. The kinetic theory assumes that there
is no force of attraction between the particles in a gas. If this
assumption were correct, gases would never condense to form liquids and
solids at low temperatures. In 1873 the Dutch physicist Johannes
van der Waals derived an equation that not only included the force of attraction
between gas particles but also corrected for the fact that the volume of
these particles becomes a significant fraction of the total volume of the
gas at high pressures. The van der Waals equation is used today to
give a better fit to the experimental data of real gases than can be obtained
with the ideal gas equation. But that wasn't van der Waals's goal.
He was trying to develop a model that would explain the behavior of liquids
by including terms that reflected the size of the atoms or molecules in
the liquid and the strength of the bonds between these atoms or molecules.
The weak intermolecular bonds in liquids and solids are therefore often
called van der Waals forces.
There are two main types of Van der Waals forces.
a) London Dispersion Forces (LDF)
These are extremely weak forces of attraction between
instantaneous dipoles called an inductive dipole which is created by a
momentary unequal distribution of electrons within one atom of a molecule.
Thus, due to the random motion of electrons around atoms, atoms can have
very slight partial charges. Imagine if more electrons are orbiting
on one side of an atom than another, this would create slight partial charges.
This force of attraction is present in all molecules but is the only force
in effect with nonpolar molecules. The duration or strength of the
force increases with the number of electrons and the size of the atoms
involved. These fluctuations in electron density occur constantly,
creating an induced dipole-induced dipole force of attraction between pairs
of atoms. As might be expected, this force is relatively weak in helium
-- only 0.076 kJ/mol. This explains the fact that helium becomes
a liquid at temperatures below 4.2 K. By itself, a helium atom is
perfectly symmetrical. But movement of the electrons around the nuclei
of a pair of neighboring helium atoms can become synchronized so that each
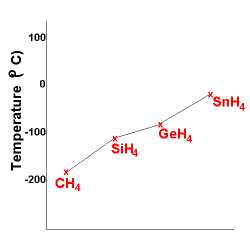
atom simultaneously obtains an induced dipole moment. As atoms become larger
and/or have more electrons, the number of inductive dipoles increases.
As you can see below, the larger atoms have more
LDF's and as a result have higher boiling points.
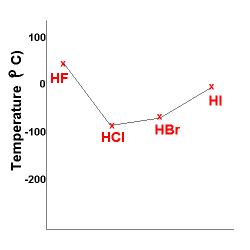
 The same trend can be seen below, except HF is an exception
since this molecule has hydrogen bonding resulting in a very strong intermolecular
attraction.
The same trend can be seen below, except HF is an exception
since this molecule has hydrogen bonding resulting in a very strong intermolecular
attraction.
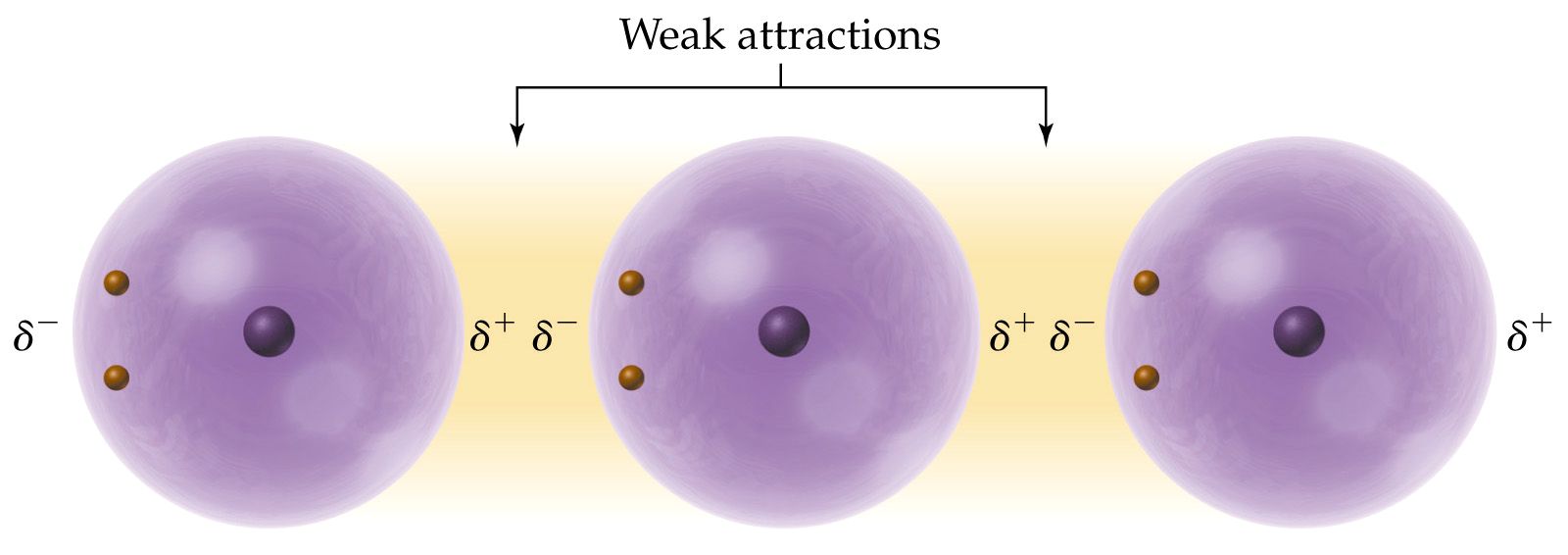
 b) Dipole - Dipole Forces:
b) Dipole - Dipole Forces:
Many molecules contain bonds that fall between the
extremes of ionic and covalent bonds. The difference between the
electronegativities of the atoms in these molecules is large enough that
the electrons aren't shared equally, and yet small enough that the electrons
aren't drawn exclusively to one of the atoms to form positive and negative
ions. The bonds in these molecules are said to be polar, because
they have positive and negative ends, or poles, and the molecules are often
said to have a dipole moment. HCl molecules, for example, have a
dipole moment because the hydrogen atom has a slight positive charge and
the chlorine atom has a slight negative charge. Because of the force
of attraction between appositely charged particles, there is a small dipole-dipole
force of attraction between adjacent HCl molecules.
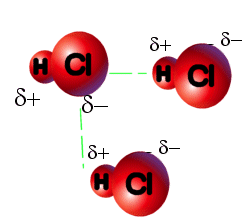
The dipole-dipole interaction in HCl is relatively
weak; only 3.3 kJ/mol. (The covalent bonds between the hydrogen and chlorine
atoms in HCl are 130 times as strong.) The force of attraction between
HCl molecules is so small that hydrogen chloride boils at -85oC.
This dipole-dipole interaction is the attraction
of a partial charge of an atom in one molecule for the opposite partial
charge on an atom in another molecule. These forces of attraction
are stronger than LDFs because they are permanent and found with polar
molecules. The stronger the dipole the greater the dipole force of
attraction.
Dipole - dipole forces involving hydrides of F, O,
and N appear to be stronger than anticipated. As a result, this particular
dipole-dipole force of attraction is specifically called a hydrogen bond.
Keep in mind that this is not really a bond but the force is collectively
strong as there is so many of them that it acts like a bond. Without
hydrogen bonding, water would not be a liquid at room temperature as it
would boil at - 80°C. It also accounts for why ice floats rather
than sinking as the water molecules cool they eventually spread out more
due to the extensive network of hydrogen bonding.
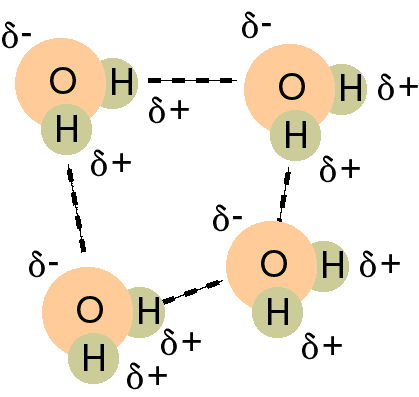
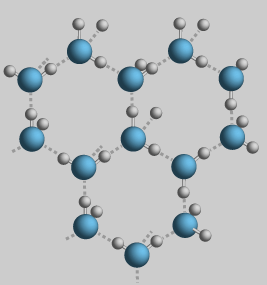
Hydrogen bonding is of extreme importance in biochemistry,
i.e. proteins, DNA etc. People with naturally curly hair have disulphide
linkages (S-S between the protein strands), but people with straight hair
who blow dry it with a curl are creating curls due to hydrogen bonding
and that is why it flattens when it gets wet.
What would happen if we mixed HCl with argon, which has
no dipole moment? The electrons on an argon atom are distributed
homogeneously around the nucleus of the atom. But these electrons
are in constant motion. When an argon atom comes close to a polar HCl molecule,
the electrons can shift to one side of the nucleus to produce a very small
dipole moment that lasts for only an instant. By distorting the distribution
of electrons around the argon atom, the polar HCl molecule induces a small
dipole moment on this atom, which creates a weak dipole-induced dipole
force of attraction between the HCl molecule and the Ar atom. This
force is very weak, with a bond energy of about 1 kJ/mol.
Since all van der Waals attractions are considerably
weaker than ionic intermolecular forces of attraction, the properties of
non-ionic solids varies and is the pretty much the opposite to those with
ionic intermolecular bonds.
-
Low melting points and boiling points because a relatively small amount
of energy is required to overcome the weak attractions between covalent
molecules, so these compounds melt and boil at much lower temperatures
than metallic and ionic compounds do. In fact, many compounds in
this class are liquids or gases at room temperature.
-
Low enthalpies of fusion and vaporization since less energy is needed to
organize the molecules and hold them in a lattice structure. These
properties are usually one or two orders of magnitude smaller than they
are for ionic compounds.
-
Soft or brittle solid forms since it is easy to break their weak intermolecular
forces. This makes the solid form of covalent molecular compounds
easy to distort or break and makes them volatile.
-
Poor electrical and thermal conductivity due to the lack of ion formation.
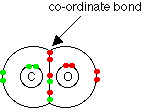
Coordinate Covalent Bonding
Coordinate covalent or dative bonding is often described
in a simple fashion by saying that it involves one atom donating or giving
a pair of electrons to another, so that this bonding partner can have a
full outer shell. When electrons are counted up in an electronic
dot diagram, this coordinate covalent pair is counted with each of the
atoms. It is similar to borrowing a pair of books from the public
library in that the books are given to you and you treat them essentially
as if they belonged to you; yet at the same time the books are counted
as being part of the library collection.
If these colourless gases are allowed to mix, a thick
white smoke of solid ammonium chloride is formed.
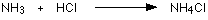
Ammonium ions, NH4+, are
formed by the transfer of a hydrogen ion from the hydrogen chloride
to the lone pair of electrons on the ammonia molecule.
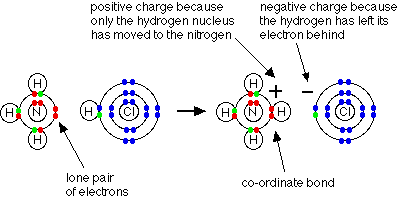
When the ammonium ion, NH4+,
is formed, the fourth hydrogen is attached by a dative covalent bond, because
only the hydrogen's nucleus is transferred from the chlorine to the nitrogen.
The hydrogen's electron is left behind on the chlorine to form a negative
chloride ion. Once the ammonium ion has been formed it is impossible
to tell any difference between the dative covalent and the ordinary covalent
bonds. Although the electrons are shown differently in the diagram, there
is no difference between them in reality.
In simple diagrams, a co-ordinate bond is shown by
an arrow. The arrow points from the atom donating the lone pair to
the atom accepting it.
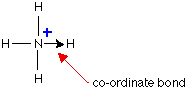
However, since the bond is identical to all the other
covalent bonds (this is known by comparing the lengths of the bonds), it
can be treated as a regular bond and the charge (if any) of the molecule
is "experienced" by the entire molecule. Often, square brackets are
drawn around the molecule and the charge is placed outside the brackets.
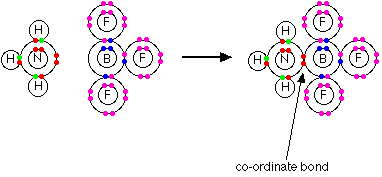
Basically, a coordinate covalent bond can occur if
there is an atom with lone paris of electrons and another atom with an
empty orbital to accept this lone pair of electrons. Consider the
following bonding:
Consider HNO3. In this case, one
of the oxygen atoms can be thought of as attaching to the nitrogen via
a co-ordinate bond using the lone pair on the nitrogen atom.
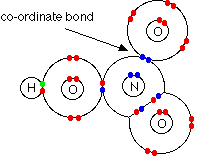
In fact this structure is misleading because it suggests
that the two oxygen atoms on the right-hand side of the diagram are joined
to the nitrogen in different ways. Both bonds are actually identical
in length and strength, and so the arrangement of the electrons must be
identical. There is no way of showing this using a dots-and-crosses
picture. The bonding involves delocalisation in that the oxygen atom
at the top relocated its electrons to create a completely free orbital
to allow coordinate covalent bonding. In a similar fashion
carbon monoxide can be thought of as having two ordinary covalent bonds
between the carbon and the oxygen plus a co-ordinate bond using a lone
pair on the oxygen atom.
Molecular Shape
We use VSEPR theory (Valence
Shell
Electron
Pair
Repulsion)
to predict the shapes of molecules. This theory predicts that bonding
and non-bonding electron pairs in a molecule will adopt a geometry in which
the distance between the electron pairs is maximized from one another in
order to minimize the repulsions. This will result in a molecular
geometry with the lowest possible energy. The theory also allows
us to predict which hybridization the central atom takes in bonding to
other atoms.
To start, we need to know the Lewis structure of
a molecule. Then we count how many pairs of electrons (triple bonds
are counted as one pair) are around the central atom. If there are
two pairs of electrons, they must be positioned 180° apart from each
other and the shape is therefore linear. Three pairs are best positioned
120° apart and the shape is thus trigonal planar. Here the shape
is referred to include the non-bonding electron pairs. For the shape
of a molecule without counting non-bonding electron pairs, make a normal
prediction then look at the molecule without non-bonding electrons showing.
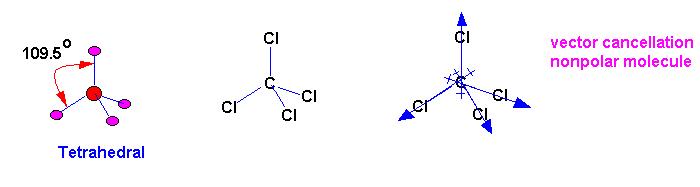
Four pairs of electrons are best positioned as tetrahedral shape.

Handling lone pairs is not as tricky as it might
sound since molecular geometries are really just special cases of the parent
electronic geometry. Since the molecular geometry is determined by
how many bonding and non-bonding electron groups surround the central atom,
the first thing one needs to do is count how many of each there are.
There is a notation that simplifies this bookkeeping: ABxEy.
The A represents the central atom, B represents the electron groups that
form bonds to other atoms, and E represents the non-bonding electron groups.
The subscripts, x and y, indicate how many of each kind are present.
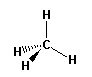
AB4
bonding groups: 4
non-bonding groups: 0 |
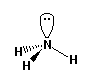
AB3E
bonding groups: 3
non-bonding groups: 1 |
AB2E2
bonding groups: 2
non-bonding groups: 2 |
|
e.g. CH4 methane |
e.g. NH3 ammonia |
e.g. H2O water |
 |
 |
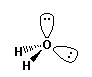 |
Depending upon the number of non-bonding electron
pairs, the shape of the molecule not counting non-bonding electron pairs
can be: a) tetrahedral (no non-bonding pairs); b) trigonal pyramidal (one
non-bonding pair); or c) "bent" or "V" (two non-bonding pairs). However,
these are all derivatives of the tetrahedral design.
Only single bonds contribute to shape so the second
bond of a double bond or second and third bond of a triple bond can be
ignored and not counted as a bonding pair. Thus carbon dioxide is
a linear molecule. AB2 , bonding groups: 2, non-bonding
groups: 0,
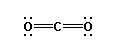
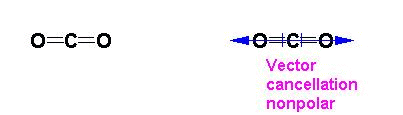
Once the shape of a molecule is determined, the question
arises as to what happens with polar bonds within this molecule.
If the molecule is made up of 2 atoms only, the polarity of the bond makes
the entire molecule polar. Likewise, a non-polar bond makes the entire
molecule nonpolar. However, what if the molecule has more than 2
atoms? A non-polar molecule has no net dipole by definition.
That is, the molecule has no distinctive poles of differing polarity.
This can be achieved by the molecule having only non-polar bonds or polar
bonds arranged symmetrically so that the dipoles cancel out.
In the first case, a molecule such as H-H or Cl-Cl
would be non-polar because the bonds are not polar. If we consider
CCl4, the bonds are polar due to the high electronegativity
of Cl and the shared electrons are pulled closer to Cl on average making
Cl partially negative and C partially positive. However, the entire
molecule is not polar since the vectors of the bond polarity cancel or
do not sum in any net direction.
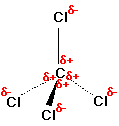
Each C-H bond is polar since carbon is more electronegative
than hydrogen (although technically not polar due to an electronegativity
under 0.4), however, each C-H bond in CH4 is arranged symmetrically
(all angles are 109.5 degrees) so that the dipoles cancel out resulting
in no net dipole for the molecule.
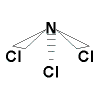
If we consider NCl3, the electronegativities
of N and Cl are similar such that the electronegativity difference is under
0.4 as well, but more on this later and the result is a non-polar molecule
as there are no polar bonds present.
A polar molecule has a net dipole. This is achieved
in the molecule by the molecule being made up of polar bonds arranged unsymmetrically
so that the dipoles do not cancel out. Consider HCN:

Both the C-H and the C-N bonds are polar. Nitrogen
is more electronegative than carbon which is more electronegative than
hydrogen. So that the hydrogen takes on a partial positive charge
and the nitrogen takes on a partial negative charge. This results
in an unequal sharing of the bonding electrons resulting in a net dipole
for molecule since the two dipoles do not cancel out.
Consider some more examples:

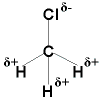
CH3Cl is a polar molecule with a net vector
pointing up to the Cl atom. The next question that arises deals with
what would happen if all of the atoms had the same general electronegativity
but differ in strength. If you know physics, you know that vectors
have two components: direction and magnitude. So far we have
not dealt with the magnitude of the bond vectors as we have only been using
predicted electronegativities based on periodic table positioning or we
have been using simple bond polarities. Consider the case where the
H's in the above diagram were replaced with bromine atoms. Bromine
is more electronegative than C and would have a partial negative charge.
However, the magnitude of the vector pointing toward Cl (C-Cl) would be
larger than the magnitude of the a single C-Br vector. It becomes
difficult to rectify how all the vectors sum, but they do not cancel so
although it may seem that this molecule would be non-polar it would in
fact be slightly polar as there is a difference in the relative strength
of the poles within the molecule. Most books do not consider the
actually electronegativities, but rather avoid the entire issue.
Consider a simple example: A--B--C, where both A and C are more electronegative
than B. Thus, A and C would be partially negative and have a vector
pointing from B to them. However, what if A was more electronegative
than C, then the magnitude of the B-A vector would be larger than the B-C
vector and they would not cancel even thought they are pointing in opposite
directions. Thus, the molecule would be polar as one side is slightly
more partial positive (less partial negative) than the other side.
References
http://www.elmhurst.edu/~chm/vchembook/201Lewisdiag.html
http://hyperphysics.phy-astr.gsu.edu/hbase/chemical/lewis.html#c2
http://www.chem.queensu.ca/people/faculty/mombourquette/FirstYrChem/Molecular/Lewis/
http://www.science.uwaterloo.ca/~cchieh/cact/c120/bondel.html
http://users.rcn.com/jkimball.ma.ultranet/BiologyPages/E/Electronegativity.html
http://www.chemguide.co.uk/atoms/bonding/electroneg.html
http://www.saskschools.ca/curr_content/chem20/covmolec/prcntion.html
http://www.bcpl.net/~kdrews/bonding/bonding2.html
http://chemed.chem.purdue.edu/genchem/topicreview/bp/intermol/intermol.html
http://www.teachmetuition.co.uk/Chemistry/Intermolecular/dipole.htm
http://hyperphysics.phy-astr.gsu.edu/hbase/chemical/waterdens.html
http://www.saskschools.ca/curr_content/chem20/ionicpds/physans.html
http://antoine.frostburg.edu/chem/senese/101/solids/faq/properties-of-molecular-compounds.shtml
http://sciencepage.org/anlchbd.htm
http://www.chemguide.co.uk/atoms/bonding/dative.html
http://www.uwosh.edu/faculty_staff/xie/tutorial/vsepr.htm
http://scidiv.bcc.ctc.edu/wv/5
http://www.ausetute.com.au/molpolar.html
http://www.ausetute.com.au/intermof.html
http://onsager.bd.psu.edu/~jircitano/polar.html



