Describing Amount of Solute in A Solution

     The concentration of a chemical substance expresses the amount of a substance present in a mixture. There are many different ways to express concentration.   Chemists use the term solute to describe the substance of interest and the term solvent to describe the material in which the solute is dissolved. For example, in a can of soda pop (a solution of sugar in carbonated water), there are approximately twelve tablespoons of sugar (the solute) dissolved in the carbonated water (the solvent).  In general, the component that is present in the greatest amount is termed the solvent. However, for most solution, regardless of amount, if water is present then water is considered to be the solvent. Therefore, it a solution was 95 % solute and water was present, water is still the solvent.

     A lot of the methods used to express solute concentrations have specific uses or references.  This means that different version of the same information exist and are used for unique reasons.  This can seem contradictory or at the very least, confusing.  The real trick to fully appreciating these formulas is to appreciate the units involved as that often indicates what information is being conveyed.

     Probably the easiest method to describe amount of solute within a solution would be the mass fraction which is simply the mass of a constituent divided by the total mass of all constituents in the mixture.  The formula is as follows:


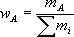
     This formula can yield a variety of units and therefore is not used to any large extent in chemistry.  However, it works well in industrial settings where it can be followed as a recipe to make a desired solution.  For example, if you needed to make a solution that contained 10 grams of salt for every kg of solution, the mass fraction would be 10 g/Kg; thus, the mass fraction can be used with little interpretation. However, if you needed to know how much water was added, you would have to some math first.  It is easy to determine if the two components are salt and water (990 g of water then), but much more difficult if other components are present, in which case the mass fraction is best.  For example, if you needed to ensure that there was 10 g of salt per every kg of prepared solution then all you do is place a container on a scale add 990 g of solution and then 10 g of salt.  If on the other hand you needed to make sure that the solution was 10% salt and the solution already had other components present, the mass fraction would be less than ideal.

     Closely related to this is %W/V or percent mass by volume.  In this case the mass of solute is given per volume of solvent.  This formula is unusual because it is one of the few formulas in which the units are mixed.  For example, a solution may be 20 % mass by volume.  This means that for every 100 mL (for example) of solvent, there will be 20 g of solute.  Mathematically the units do not cancel, but the formula is useful because it allows solutions to be created very quickly.  I used it often when I worked in industry.  I would just work out how many grams of solute was needed to be added to a certain volume of water.  It is fast and easily repeated. 



      More typically, chemists rely on percent by mass (%W/W) or percent by volume (%V/V).  In both cases, the units for the solute and the solution are the same.  In both cases, the formula uses an amount of solute (mass or volume) divided by an amount (mass or volume respectively) of solution. 



      Typically %W/W is used when the solute is a solid and %V/V is used when the solute is a liquid.  However, occasionally, %W/W can be used for liquid solutes.  Care must be take when using these formulas since the amount of solution equals the combined mass or volume of solute and solvent.  Thus, if you were asked to determine the amount of water needed to make a 20% by volume solution using 10 mL of alcohol, the required amount of water would be 40 mL (10 + 50) and not 50 mL as many people assume.  This is because 10/50 x 100 = 20% which means that 50 mL of solution = 10 (solute) + 40 (water).  Also, since pure water has a density of approximately 1.0 g/mL, mL and g of water can be used interchangeably as needed.

      Often one encounters solutions in which the percent solute is extremely low.  Intuitive you would think this is rare, but extremely small concentrations of solute can have devastating effects.  For example, 0.0107 % by mass of HCN can kill an average adult in 10 minutes of exposure.  Acrylonitrile, C₃H₃N, can lead to cancer, neurological and reproductive failure or death at levels 0.0002 % - 0.01 % by mass.  Household chemicals also pose similar risks.  For example tetrachloroethylene, is known to cause (based largely on animal studies):

• death
• intense irritation of the upper respiratory tract and eyes, kidney dysfunction, and neurological effects such as reversible mood and behavioral changes, impairment of coordination, and anesthetic effects
• effects on the liver, kidney, and central nervous system (CNS)
• neurological effects, including headaches, and impairment of memory, concentration, and intellectual function
• menstrual disorders and spontaneous abortions
• birth defects
• increased incidence of a variety of tumors
• increased risk of childhood leukemia
• liver cancer and some may have mutagenic activity      

      The threshold for human safety for tetrachloroethylene seems to be about 140mg/m₃ or about 0.002058% by mass.   Tetrachloroethylene is used in dry cleaning and carpet and upholstery shampoos.  It is very toxic!

      Another dangerous household chemical is, acrylamide.  It is known to cause (based largely on animal studies):

• skin and respiratory tract irritant
• general systemic toxicity and changes in hematological parameters
• neurotoxicant
• perineal soiling, depletion of adipose tissue, decreased liver size, darkened kidneys, mottled lungs, atrophy of skeletal muscle, distention of urinary bladder, and thickening of the stomach; decreases in packed cell volume, total erythrocyte counts and hemoglobin concentrations
• decreased body weight
• causes a variety of tumors
• possibly carcinogenic to humans
• chromosomal aberrations, dominant lethality, sister chromatid exchanges and unscheduled DNA synthesis
• testicular atrophy and decreased fertility have been reported in male mice
• drowsiness, hallucinations, distal numbness, and ataxia
• paresthesias in the fingers, coldness, numbness in lower limbs, and weakness of the hands and feet
• polyneuropathy with motor and sensory impairment marked by numbness, paresthesias, ataxia, tremor, dysarthria, and mid- brain lesions
• disturbances of balance, confusion, memory loss
• axon and myelin degeneration
• EEG abnormalities
• severe muscle weakness
• visual acuity and contrast sensitivity were decreased

      Acute toxicity of acrylamide in rats has been found to be 400 mg/Kg of body weight.  A serving of french fries or potato chips can contain 1.4 % by mass of acrylamide.  Yum!

      These numbers are so small that it is often more convenient to express them as fractions of a larger total.  Statistics are often done this way as well; for example, on average, 6 out of every 100 males has red-green colourblindness.  This would be 6 parts per 100.  In chemistry, we need considerably smaller measurements such as parts per million (ppm) or parts per billion (ppb)or parts per trillion (ppt) and etc.  1 ppm = 1 g of solute in 1 million g of solution, but since there is so little solute compared to amount of solution, we really just consider the amount of solute/amount of solvent; therefore, 1 ppm = 1 g of solute/1 million mL of water (remember 1 mL = 1 g of water).  As long as the difference between the amount of solute and the amount of solvent is 1 million, it is a ppm (keeping the units the same, of course).

      A solution with a concentration of 1 ppm has 1 mg of substance for every million mg of water.  A mg of water though is really just 1 L of water (density = 1 g/mL).  Therefore, in general, one ppm implies one milligram of solute per 1000 mL or 1 L of water.  Finally, recognize that one percent = 10,000 ppm.  Therefore, something that has a concentration of 300 ppm could also be said to have a concentration of (300 ppm)/(10,000 ppm/percent) = 0.03% percent by mass.   Parts per billion (ppb) works like above, but we multiply by one billion (10⁹).  A solution with 1 ppb of solute has 1 microgram (10⁶ g) of material per L of water.  Parts per trillion (ppt) works like parts per million and parts per billion except that we multiply by one trillion (10¹²).

 
Types of Solutions

     Solutions can be distinguished by the amount of solute they contain.  In actuality, they are not different types, but merely different conditions of the same solution.  For example, a 1% W/W solution is not really a different solution than a 5% W/W solution.  However, we typically do distinguish amongst extreme variations because their properties become quite different.  Any properties that change when the concentration of a solution changes are called colligative properties.  Based on these extreme difference, three types of solutions can be distinguished. 

• unsaturated:  This means that if you were to add more solute to the liquid, it would keep dissolving.  For example, if you take one teaspoon of salt and put it in a bucket of water, you've made an unsaturated solution.  (In other words, if you added another teaspoon of salt, it would dissolve, too).
• saturated:  This means that the liquid has dissolved all of the solute that is possible.  If any of you have a little brother or sister who adds sugar to iced tea, you know what I'm talking about.  If you add one teaspoon of sugar to iced tea, you've got an unsaturated solution.  If you keep adding sugar to iced tea, you eventually get to the point where the rest of the sugar just sinks to the bottom.  When this happens, it means that the solution is saturated, because no more sugar could dissolve.
• supersaturated:  This means that more solute has dissolved than is possible.  How, you might ask, does this happen?  If you have a very hot saturated solution and cool it down, the solubility of the solute decreases as the solution cools.  (In other words, hot solutions can dissolve more solute than cold ones).  What usually happens in this situation is that the solute starts forming crystals at the bottom of the container.  However, under weird circumstances where there are no little grains to start crystal formation, the crystals never form - as a result, the solution is more concentrated than possible.  This doesn't happen much, so you'll rarely never run into it in everyday life.

      Consider the typical solubility curve for a solute (recall that solidity of most solids increases as temperature increases).
     
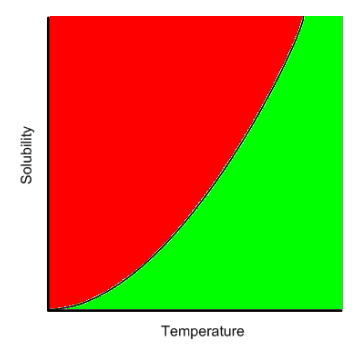
      If the amount of solute dissolved into the solvent results in a solution with a solubility on the line in the middle of the curve, then the solution is saturated as this is the maximum amount of solute that can be dissolved at that temperature.  If, however, the amount of solute dissolved in the solvent creates a solution with a solubility below that line (green area) then the solution is unsaturated as more solute could dissolve at that temperature (until the solubility hits the line).  On the other hand, if the solubility is above the line (red area) then more solute was dissolved than typically possible at that temperature and the solution is supersaturated.  If a solution is supersaturated, it can be easily converted to a saturated solution.  Anything that can disrupt the lattice network of the solution (agitation, scratching the inside of the container, dropping a solid (seed) crystal into the solution) and the excess solute will solidify (precipitation) and collect at the bottom of the container.  The solution will precipitate all the excess solute out of solution leaving behind a saturated solution with a solid mass in the container.

      Solubility curves differ from substance to substance based on how a solid lattice can be broken up by the solvent to create a solution lattice structure.  Consider some examples:


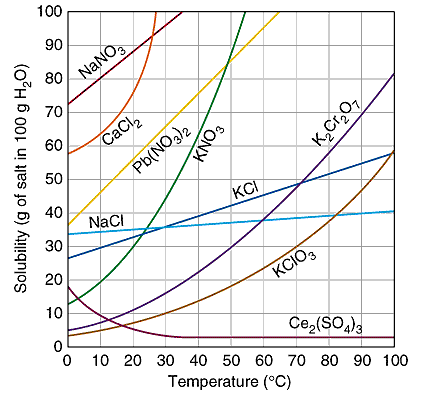
     As you can see some substance are more soluble than others. For some substances, solubility increases with temperature in a linear fashion, but for others it can be exponential.  There is no trend.  To create a solubility curve, you must determine the maximum amount of solute that can dissolve in a defined amount of solvent; typically g/100 g of water.  This process is repeated over a range of temperatures; typically from 0ºC to 100ºC.  The data is plotted on a solubility versus temperature graph.   

     A solubility graph can be used to identify a substance by comparing the solubility of your unknown to the known curves.  For example, what substance has a solubility of 90 g/100 cm3 of water at a temperature of 25ºC?  The only substance whose solubility curve is located at the intersection of 90 g/100 cm3 and 25ºC is sodium nitrate.  You can also use the solubility curve to derive unknown information.  For example,what is the solubility of potassium nitrate at 80ºC ? Locate where 80ºC is on the solubility curve for potassium nitrate. Extend a line over to the solubility axis that is level with this point. If you did it correctly,the solubility should be 170 grams.  Or, for example, at what temperature will sodium nitrate have a solubility of 95 g/100 cm3 ? You'll need to more carefully estimate where 94 g will be,but if you drop a vertical line down from this intersection point,it should be about 30ºC.

     When solving questions like these, it is important to make sure the units of the question match those of the solubility curve.  For example, if you were asked whether 3.7 g of KCl added to 12 mL of water was unsaturated, saturated or supersaturated at 50ºC, you must first use ratios to convert these units to match the graph above.  In this case:

3.7 g	dissolved in	12 mL
X g	dissolved in	100 mL

     Solving this ratio reveals that dissolving 3.7 g of KCl in 12 mL of water is really the same as dissolving 30.83 g in 100 mL.  Looking at the graph above, you can see that this means the resulting solution is unsaturated at 50ºC.

     Sometimes you'll need to determine how much additional solute needs to be added to a unsaturated solution in order to make it saturated.  For example, 30 grams of potassium nitrate has been added to 100 mL of water at a temperature of 50ºC.  From the graph you can see that the solubility for potassium nitrate at 50ºC is 84 grams.  If there are already 30 grams of solute in the solution, all you need to get to 84 grams is 54 more grams (84 g - 30 g).

     Lastly you can use a solubility graph to determine at what temperature a precipitate (crystals) will begin forming when an unsaturated solution cools down.  Suppose you have a 100 mL KClO₃ solution at 100ºC containing 50 g of dissolved solute. Locate where 50 g intersects the curve for KClO₃ and the temperature at this point is when crystals can start forming.  In this example the temperature will be about 93ºC.  Or, you may be asked to determine the amount of precipitate that would be collected if this solution was cooled to 30ºC.  At 30ºC, the maximum solidity is 10 g/100 mL and if the original solution contained 50 g, 40 g of precipitate could be filtered out of the container.

 

 
Molarity

    Another way of expressing concentration, the way that is most preferred in chemistry, is called molarity.  Molarity is the number of moles of solute dissolved in one liter of solution. The units are moles per liter; specifically it's moles of solute per liter of solution which can be expressed simply as M.   The formula is M =n/V .

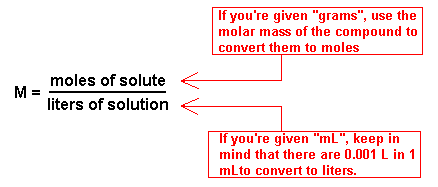
    There are several types of calculations that you need to be able to do with molarity.   First, you should be able to manipulate the formula to solve for one of the missing variable.  For example, you should be able to calculate the molarity if you are given the components of the solution.  For example, what is the molarity of a NaCl solution if 0.32 moles of NaCl is added to 3.4 L of water (recall that adding solids to liquids does not change the volume substantially).  To get the polarity we need to divide the number of moles of NaCl by the volume of the solution.  In this case that is 0.32 moles NaCl divided by 3.4 L, and that gives 0.094 M NaCl.  You could also solve for moles or volume directly using the polarity formula.

    You could also be asked to manipulate and apply the polarity formula.  For example, you could calculate the amount of solute in (or needed to make) a certain volume of solution.   For example, how would you prepare 400 ml of 1.20 M solution of sodium chloride?   1.20 M NaCl means there is 1.2 moles of NaCl per 1.00 liter of solution.  Use the polarity formula to determine the moles of NaCl needed to make up a 400 mL solution.

M = n/v, but we rearrange this to solve for moles

n = MV = (1.2 mol/L)(0.4 L) = 0.48 moles of NaCl are needed

n = m/mm so m = n(mm) = (0.48 mol)(58.5 g/mol) = 28.1 g

    Therefore, dissolve 28.1 g of NaCl in 400 mL of water to make 400 ml of 1.20 M solution of sodium chloride.  You could also be asked to find density and etc.

    Typically, you need to be able to convert one polarity into another, often done by completing a dilution of the original solution.  This math is not as hard as it might seem.  Since water is being added, moles of solute remain constant which means the moles of solute before the dilution = the moles of solute after the dilution.  Often the original solution is denoted by a subscript of 1 and the final solution is denoted by a subscript of 2.  Also, we know that for solutions moles of solute = polarity x volume (see polarity formula above).  Thus the dilution equation can be found:

moles before	=	moles after
M1V1	=	M2V2

    You can use this dilution equation to solve for an unknown as long as only the amount of solvent is changing.  For example, a chemist starts with 50.0 mL of a 0.40 M NaCl solution and dilutes it to 1000 mL. What is the concentration of NaCl in the new solution?

M1V1	=	M2V2
(0.40 M) (50.0 mL)	=	M2(1000 mL)
(0.40 M) (50.0 mL) (1000mL)	=	M2
0.020 M	=	M2

    Notice that unlike the polarity equation, the dilution equation does not have to be in L as long as the volumes of both sides of the equation have the same units (they will cancel).

    Polarity allows us to do stoichiometric calculations when the reaction occurs in solution.  Working stoichiometry problems using solutions isn't much harder than a normal stoichiometry problem.  Rather than using the molecular weight to convert a weight to moles, you use the volume and polarity of the solutions to get the moles of the reactants.  Once you have that, you can work out the moles of products normally.

    If you mix 200 ml of 0.100 M Pb(NO₃)₂ and 300 ml of 0.200 M NaCl, how much PbCl₂ precipitate will you form?

1. Balance the equation.

• Pb(NO₃)₂  +  2 NaCl    PbCl₂  + 2 NaNO₃

2. Find moles of each reactant

• moles of Pb(NO₃)₂:  n = MV = (0.1)(0.2) = 0.02 mol
• moles of NaCl: n-MV = (0.2)(0.3) = 0.06

3. Find limiting moles.

• Pb(NO₃)₂:  0.02/1 = 0.02 mol
• NaCl:  0.06/2 = 0.03 mol; therefore Pb(NO₃)₂ limits

4. Conduct stoichiometric calculations.

• 1 mole of Pb(NO₃)₂ yields 1 mole of PbCl₂
• 0.02 mole of Pb(NO₃)₂ yields x moles of PbCl₂
• therefore x = 0.02 moles of PbCl₂

5. Find mass.

• n = m/mm; therefore, m = n(mm) = 0.02(278.1) = 5.56 g of PbCl₂

    These types of molar stoichiometry questions can be combined with any other stoichiometric calculations already learned.

Titration

    One specific type of solution stoichiometric calculation that is of critical importance is titration.  Titration is a laboratory technique by which the concentration of an unknown solution can be determined by using a standard concentration of another reagent that chemically reacts with the unknown.  This standard solution is referred to as the titrant.  We have to have some way to determine when the reaction is complete that we are using.  This is referred to as the end point.  The most typical type of titration is an acid/base titration.

    Acid-base reactions are ubiquitous.  In aqueous solutions acids increase the hydrogen ion (H⁺) concentration.  On the other hand bases increase the hydroxide ion (OH^-) concentration.  When an acid and a base react in an aqueous solution the H⁺ and OH^- ions combine to form water.  These ions thus "neutralize" one another: 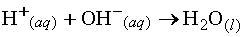.  Really though we must include the hydronium ion:

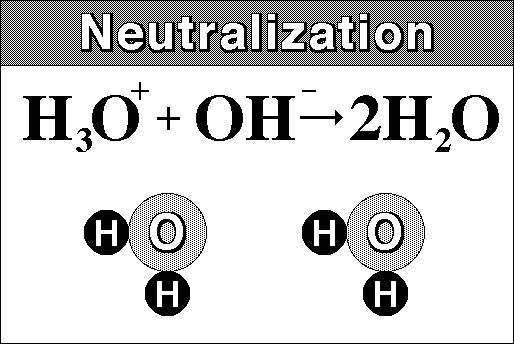
    A salt is any compound which can be derived from the neutralization of an acid and a base.  A neutralization is a type of double replacement reaction. 

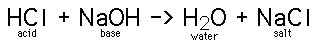
    When acids and bases are mixed together, they can either completely neutralize each other or partially neutralize each other.  In the case of complete neutralization, the moles of H⁺ and OH^- equal each other.  In a titration one reagent, the titrant, is added to another slowly.  As it is added a chemical stoichiometric reaction occurs until one of the reagents is exhausted, and some process or device signals that this has occurred.  The purpose of a titration is generally to determine the quantity or concentration of one of the reagents, that of the other being known beforehand.  In any titration there must be a rapid quantitative reaction taking place as the titrant is added, and in acid-base titrations this is a stoichiometric neutralization. 

    All acid-base titration reactions, as all acid-base reactions, are simply exchanges of protons.  The reaction could be strong acid + strong base as in the case of HCl + NaOH above. Virtually all acid-base titrations are carried out using a strong acid or strong base.  In most cases the strong acid or strong base is used as the titrant.  It is less common, but equally feasible, to place the strong acid or strong base in the titration vessel and use the weak acid or weak base as the titrant.  A weak acid-weak base titration would have only a small pH change at the equivalence point.  This small change is difficult to detect, and for this reason weak acid-weak base titrations
are uncommon. 

    One of the substances involved in a titration must be used as a standard for which the amount of substance present is accurately known.  The standard can be present either in the form of a pure substance or as a standard solution, which is a solution whose composition is accurately known.  A standard can be prepared in only two ways: use a primary standard or standardize by titration against some previously standardized solution.  A primary standard is some substance such as oxalic acid which can be precisely weighed out in pure form, so that the number of moles present can be accurately determined from the measured weight and the known molar mass.  For example, we might prepare a 0.1000 molar solution of primary standard oxalic acid by weighing out exactly 0.1 moles of oxalic acid and diluting to one litre in a volumetric flask. 

    The standard solutions used in an acid-base titration need not always be primary standards.  A standard solution which has been prepared by quantitative dilution of a primary standard is an excellent secondary standard solution.  Secondary standards can also be prepared by titration against a primary standard solution. 

    To titrate an unknown acid/base solution, take a certain amount of the unknown solution and add a standard reagent of the known concentration carefully until the neutralization reaction is completed.  This point where the number (or mole) of hydrogen ions and hydroxide ions are equal is defined as the equivalence point.  To determine the equivalence point, scientists use an indicator or a pH meter. 

    First, you need to choose volume of an unknown acid or base solution and put it in an erlenmeyer flask.   Second, fill a buret with a standard reagent of known concentration and read the initial volume of the solution.  Of course, if you put an acid in the erlenmeyer flask, you need to put a base in the buret and vice versa.  A buret is a good apparatus for the determination of an equivalence point in acid-base titration because you can accurately read the volume of solution used.  Third, add a couple of drops of an indicator in the flask for titration.  An indicator is a soluble dye that changes its color noticeably over a fairly short range of pH.  Different indicators show color changes at different pH values and it is important to determine an indicator to be used according to the expected equivalence point.  Fourth, slightly open the stopcock of the buret and add the standard reagent into the unknown solution.  Around the expected equivalence point of the titration, you need to drop the solution very slowly and mix the solutions very well because, around the equivalence point, just one drop of solution from the buret can make a radical pH change in the mixed solution.  If the color of the solution in the erlenmeyer flask changes, record the volume of  the solution in the buret and add a few drops of the solution to make sure the equivalence point you found is correct.  Finally, using the data from your acid-base titration, you can calculate the concentration of the unknown solution.  The equation for this procedure is as follows. (Here, M means polarity (concentration) of solution , and V means volume of solution.) 

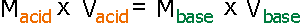
    For example, if you choose 10.0 mL hydrochloric acid solution as a concentration-unknown solution and it takes 10.0 mL of 0.100 M sodium hydroxide solution to titrate, the concentration of the hydrochloric acid is 0.100 M. 

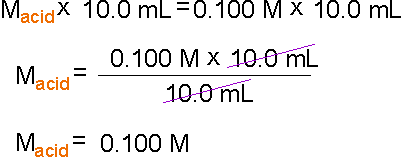
    If you want to use a polyprotic acid or base (which can donate two or more hydrogen or hydroxide ions per molecule) for titration, you need to multiply the polarity of the solution by the number of hydrogen or hydroxide ions it can donate per molecule.  For example if H₂SO₄ were used instead of HCl, M_AV_A becomes 2M_AV_A.

References

http://www.ilpi.com/msds/ref/concentration.html
http://www.iupac.org/goldbook/M03722.pdf
http://www.cdc.gov/Niosh/idlh/74908.html
http://www.lenntech.com/hazardous-substances/acrylonitrile.htm
http://www.lakes-environmental.com/toxic/TETRACHLOROETHYLENE.HTML
http://www.sciencelab.com/xMSDS-Page_8_Solution-9926370
http://www.hc-sc.gc.ca/fn-an/securit/chem-chim/acrylamide/acrylamide_level-acrylamide_niveau_e.html
http://www.buhs.k12.vt.us/science/physicalscience/Lab%20images/0009-004-sol-v-t.gif
http://www.thesciencedesk.com/sgsolubilitygraph.htm
http://patrick.wattle.id.au/cameron/cshs/hammond/weekend/ppt2.jpeg
http://dl.clackamas.edu/ch105-04/molarity.htm
http://misterguch.brinkster.net/molaritytutorial.html
http://dl.clackamas.edu/ch105-04/calculat.htm
http://dl.clackamas.edu/ch105-04/dilution.htm
http://www.iun.edu/~cpanhd/C101webnotes/aqueoussolns/solstoic.html