Elucidation of the Mole
The number of scientists that worked to identify the mole, either directly or indirectly, is actually quite large. Furthermore, it may actually be quite difficult to be certain that all the influences and connections have been properly identified since so many advances in technology and experimental evidence could play some pivotal role. This is true of most scientific investigations and theory development. Therefore, what is presented here, represents a somewhat linear and constrained view to simply show how such connections are created and impacted the determination of the chemical concept known as the mole which may be one of chemistry's most important concepts.
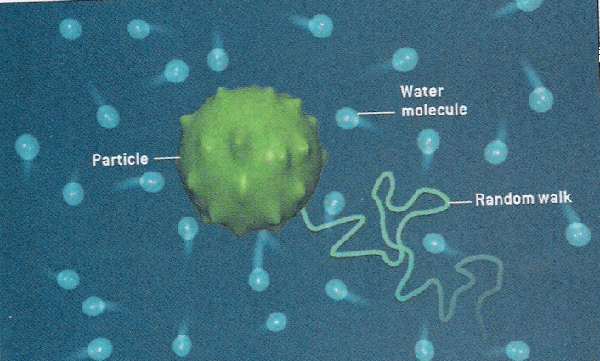
Prior to the understanding mole, there was lots of evidence for the existence of atoms, but there was a pressing need to quantify their numbers. At the time, scientists did not know how to count and thus, measure atomic quantities. One of the first lines of evidence was Brownian motion which is the erratic random movement of microscopic particles in a fluid, as a result of continuous bombardment from molecules of the surrounding medium due to their random motion. This hints at the relative number of particles involved at the microscopic level due to the number visible interactions due to collisions.
For example, if you look at fat globules in diluted milk under a microscope, the fat globules vibrate in response to water particle bombardment. Essentially, more vibration or motion indicates that the fat globules were being hit by a large number of water particles. Although, this allowed scientists to realize that the number of collisions could indicate number of particles, they did not know how to measure this since there are just too many water particles involved.
The Italian scientist, Lorenzo Romano Amedeo Carlo Avogadro, conte di Quaregna e di Cerreto (1776
- 1856),
was born in Turin, Italy, on 9th August, 1776. In spite
of a successful legal career, Avogadro also showed an interest in natural
philosophy, and in 1800 he began private studies of mathematics and physics.
In 1809 became professor of natural philosophy at the college of Vercelli.
In 1811, Avogadro published an article in Journal de physique that clearly
drew the distinction between the molecule and the atom. He pointed
out that Dalton had confused the concepts of atoms and molecules.
Dalton still equated particles with atoms, and could not accept how one
particle of oxygen could yield two particles of water. The "atoms"
of nitrogen and oxygen are in reality "molecules" containing two atoms
each. Thus two molecules of hydrogen can combine with one molecule of oxygen
to produce two molecules of water.
Amedeo Avogadro is credited with being the first person to directly address particle number and so changed the chemical world in 1811. He worked to find a way to determine particle number by comparing 2 gases at the same temperature and volume. By keeping temperature constant, he knew the particles all had the same energy for motion and by keeping volume constant, he knew that the particles were travelling the same distance and finally since gas particles are immensely small, there essentially all act the same.
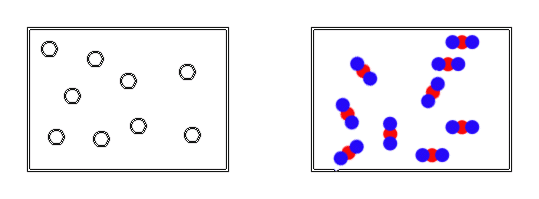
So this led to his famous hypothesis. He measured and compared the pressures generated by the gases realizing that the pressure generated by a gas is due to the incredibly large number of perfectly elastic collisions on the wall of the container. He then hypothesized that when the pressures of two gases were equal, it must be due to the fact the containers held the same number of particles when the volumes and temperature were equal. This was called Avogadro's Principle.
Now, this really is not that exciting yet, but he took it one step further. He massed the samples of gases and found that samples of gas with the same temperature, volume and pressure had different masses. He knew that if the volume was the same, the particles were travelling the same distance there should be now difference in pressure (collisions on the walls of the container) and since temperature was constant, all the particles were travelling at the same speed meaning they hit the container wall with identical force or pressure. Therefore, if the pressures were the same, the number of particles were the same and so the only difference in mass must be due to the fact that each gas particle has its own unique mass.
It was long after
Avogadro that the idea of a mole was introduced. Since a molecular weight
in grams (mole) of any substance contains the same number of molecules,
then according to Avogadro's Principle, the molar volumes of all gases
should be the same. The number of molecules in one mole is now called
Avogadro's number. It must be emphasized that Avogadro, of course, had
no knowledge of moles, or of the number that was to bear his name. Thus
the number was never actually determined by Avogadro himself. It
is a honourary accreditation to all his work.
At this point scientists still really only know relative number of particles based on comparative masses. Scientists still wanted to find a way to actually count the number of particles in any sample. In 1865, Loschmidt, an Austrian chemist devised an ingenious method to count particles using mass and pressure. He measured how much mass could be supported by a standard volume, temperature and pressure of a standard gas, like 12.00 g of carbon 12. He then worked out this mass per cm3 of standard gas at standard temperature and pressure. He did this per cm3 because he needed a way to reduce the number of particles to make the work manageable. He then mathematically and experimentally worked out the number of gas particles needed (based on the average speed of gas particles moving through a very restricted tube into the chamber from his chemical reaction) to be added per cm3 at standard temperature and pressure to suspend the same amount of mass as in the standard sample. He found it took 2.6 x 1019 particles to match the original standardized volume, temperature and pressure.
However, as impressive as the feat was, it could not be readily replicated. There were errors in the estimations used to calculate the number of particles added to the container. This does not mean it should be dismissed as it is still quite an accomplishment. In 1909, Perrin, painstakingly worked out a more accurate measurement using Brownian motion. He calculated the number of water particles that were actually needed to push a fat globule in a milk suspension a specific distance. His goal was to work out the total number of particles needed to equal the same force required to generate the standard pressure for the standardized sample of a gas. He found it took 6.2 x 1023 particles and this number has been routinely verified. It turns out to be fairly close the right answer.
The actual number is now called Avogadro’s number since he started it all. However, the accuracy has improved considerably. For quite a while a Geiger counter was used to exactly count the number of radioactive gas particles in 12.00 g of standardized carbon-12 sample which is a consistent ratio to the total number of particles present. Lately, scientists count the number of particles present in a standardized sample of solid lattice as a function of how far x-rays can be deflected.
The Mole
As we all know today, Avogadro's number is very large, the presently the most
recent, precise, verified and accepted value of the mole 6.022140857 x 1023 (it changes slightly as equipment and techniques are refined). The size of such a number is extremely
difficult to comprehend. There are many awe-inspiring illustrations to
help visualize the enormous size of this number. For example: An
Avogadro's number of standard soft drink cans would cover the surface of
the earth to a depth of over 200 miles. If you had Avogadro's number
of unpopped popcorn kernels, and spread them across the United States of
America, the country would be covered in popcorn to a depth of over 9 miles.
If we were able to count atoms at the rate of 10 million per second, it
would take about 2 billion years to count the atoms in one mole.
Cannizarro, around 1860, used Avogadro's ideas to
obtain a set of atomic weights, based upon oxygen having an atomic weight
of 16. In 1865, Loschmidt used a combination of liquid density, gaseous
viscosity, and the kinetic theory of gases, to establish roughly the size
of molecules, and hence the number of molecules in 1 cm3 of
gas. During the latter part of the nineteenth century, it was possible
to obtain reasonable estimates for Avogadro's number from sedimentation
measurements of colloidal particles. Into the twentieth century, then Mullikens
oil drop experiment gave much better values, and was used for many years.
A more modern method is to calculate the Avogadro number from the density
of a crystal, the relative atomic mass, and the unit cell length, determined
from x-ray methods. To be useful for this purpose, the crystal must be
free of defects. Very accurate values of these quantities for silicon have
been measured at the National Institute for Standards and Technology (NIST).
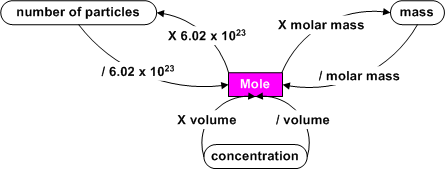
Mole Math
We know that we can find the molar mass of
a substance from the periodic table. We also know that we can find
the mass of a sample by using a balance in the laboratory. By dividing
the mass of a sample by its molar mass, we get the number of moles of the
substance.
Example 1.
If you find the mass of a sample of glucose (C6H12O6)
to be 90.0 g, how many moles of glucose do you have? We look up the
masses of each atom on the periodic table, multiply by the number of atoms
present and add the total.
Molar mass of C6H12O6 is:
Carbon = 12.0 g x 6 atoms = 72.0 g
Hydrogen = 1.01 g x 12 atoms = 12.1 g
Oxygen = 16.0 x 6 atoms
= 96.0 g
---------
180.1 g
Now use the formula:
mol = 90.0 g/180 g/mol = 0.500 mol
Example 2.
A certain laboratory procedure requires the use of 0.100 moles
of magnesium. How many grams of magnesium would you mass out on the
balance?
From the period table we get the Molar mass of magnesium as 24.3 g.
Now rearrange the formula:
mass = (mol)(molar mass) = (0.100 mol)(24.3
g/mol) = 2.43 g of magnesium
Example 3.
How many molecules of carbon dioxide are found in 2.50 moles of carbon
dioxide?
Here we recall that:
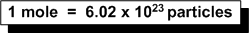
Set up a ratio:
1 mole = 6.02 x 1023 molecules/mol
2.50 mol = x molecules of CO2
Solve by rearranging:
x molecules of CO2 = (2.50 mol)(6.02 x 1023
molecules/mol) = 1.51 x 1024 molecules of CO2
Example 4.
How many moles are represented by 7.45 x 1024 molecules of
O2?
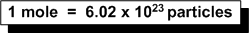
Set up a ratio:
1 mole = 6.02 x 1023 molecules/mol
x mol = 7.45 x 1024 molecules of O2
Solve by rearranging:
x moles = (1) (7.45 x 1024 molecules)/6.02 x 1023
molecules/mol = 12.4 moles of O2
You may need to convert between units such as number of particles
to mass. This can be done by first converting to moles or by working
with molar equivalents.
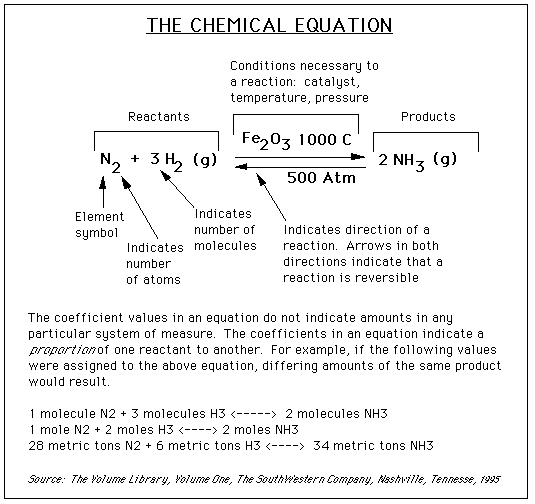
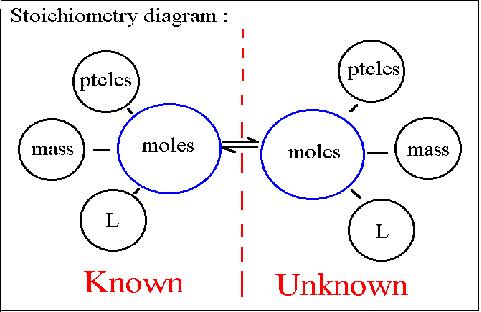
Stoichiometry
The word stoichiometry derives from two Greek words:
stoicheion (meaning "element") and metron (meaning "measure"). Stoichiometry
deals with calculations about the masses (sometimes volumes) of reactants
and products involved in a chemical reaction.
Consider an equation:
Example 1.
Given the Haber Process: N2 + 3 H2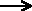
2 NH3 Determine the grams of H2 that
will react with the 4 moles of N2.
Convert moles of N2 given to moles of requested H2.
This requires the use of the coefficients of N2 and H2
from the balanced equation:
N2 + 3 H2
2 NH3
Set up the ratios:
1 mole N2 = 3 moles H2
4 moles N2 = x moles H2
Solve by rearranging:
(1 mole of N2)(x moles of H2) = (4 moles of
N2)(3 moles of H2) = 12 moles of H2
Convert the moles of requested H2 to grams of H2
using:
12 mole H2 = x grams H2/2.0 grams of H2
Solve by rearranging:
x grams of H2 = (12 moles H2)(2.0 grams
H2) = 24.0 grams H2
Sometimes the reactants for a reaction in an experiment
are not necessarily a stoichiometric mixture. In a chemical reaction, reactants
that are not use up when the reaction is finished are called excess reagents.
The reagent that is completely used up or reacted is called the limiting
reagent, because its quantity limit the amount of products formed.
Consider the reaction between sodium and chlorine. The reaction can be
represented by the equation:
2 Na + Cl2 2 NaCl
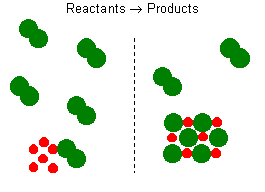This balanced reaction equation indicates that two Na atoms would
react with two Cl atoms or one Cl2 molecule. Thus, if you
have 6 Na atoms, 3 Cl2 molecules will be required. If there
is an excess number of Cl2 molecules, they will remain
unreacted. We can also state that 6 moles of sodium will require 3
moles of Cl2 gas. If there are more than 3 moles of Cl2
gas, some will remain as an excess reagent, and the sodium is a limiting
reagent. It limits the amount of the product that can be formed.
To solve these types of questions you can either use one reactant
at a time to determine which reactant produces the least amount of
product. This will represent the correct answer and the reactant
use will represent the limiting reagent. Alternatively, you
can calculate the molar ratio of each reactant by finding the moles
of each reactant and dividing by the respective numerical coefficients
from the balanced equation. The reactant with the smaller molar
amount limits the reaction and should be used for all future calculations.
References
http://www.bulldog.u-net.com/avogadro/avoga.html
http://www.paleorama.com/Eponyms-A/Amedeo_Avogadro.php
http://www.moleday.org/
http://www.visionlearning.com/library/module_viewer.php?mid=56&l=&c3
http://www.shodor.org/UNChem/basic/stoic/index.html
http://cwx.prenhall.com/bookbind/pubbooks/hillchem3/medialib/media_portfolio/03.html
