Defining Equilibrium

    Basically, the term refers to what we might call a "balance of forces".  In the case of mechanical equilibrium, this is its literal definition. A book sitting on a table top remains at rest because the downward force exerted by the earth's gravity acting on the book's mass (this is what is meant by the "weight" of the book) is exactly balanced by the repulsive force between atoms that prevents two objects from simultaneously occupying the same space, acting in this case between the table surface and the book. If you pick up the book and raise it above the table top, the additional upward force exerted by your arm destroys the state of equilibrium as the book moves upward. If you wish to hold the book at rest above the table, you adjust the upward force to exactly balance the weight of the book, thus restoring equilibrium.  An object is in a state of mechanical equilibrium when it is either static (motionless) or in a state of unchanging motion.  From the relation f = ma , it is apparent that if the net force on the object is zero, its acceleration must also be zero, so if we can see that an object is not undergoing a change in its motion, we know that it is in mechanical equilibrium.

    Consider a person on a bungee cord.  When the jump off a bridge they are not in mechanical equilibrium since the are rapidly moving towards the Earth due to gravity.  As the bungee cord extends, they reach equilibrium for an instant when the force of gravity equals the opposing force of the bungee cord retracting and the person stops moving.  However, as soon as the bungee cord retracts and the person accelerates upward, equilibrium is lost until the forces again equal at the top.  This cycle continues until the force causing the bungee cord to recoil is gone. At which point the equilibrium is permanent (more or less) and the person stops bobbing up and down (more or less).

    Another kind of equilibrium we all experience is thermal equilibrium. When two objects are brought into contact, heat will flow from the warmer object to the cooler one until their temperatures become identical. Thermal equilibrium is a "balance of forces" in the sense that temperature is a measure of the tendency of an object to lose thermal energy. A metallic object at room temperature will feel cool to your hand when you first pick it up because the thermal sensors in your skin detect a flow of heat from your hand into the metal, but as the metal approaches the temperature of your hand, this sensation diminishes. The time it takes to achieve thermal equilibrium depends on how readily heat is conducted within and between the objects; thus a wooden object will feel warmer than a metallic object even if both are at room temperature because wood is a relatively poor thermal conductor and will therefore remove heat from your hand more slowly. Thermal equilibrium is something we often want to avoid, or at least postpone; this is why we insulate buildings, perspire in the summer and wear heavier clothing in the winter.

    Many reactions in chemistry go 100% to completion such as burning methane or simple acid/base neutralizations.  However, many reactions are complete when they are in fact only partially converted to products.  These reactions exist in a dynamic state of flux in which reactants become products and products become reactants.  Previously we would have defined these reactions as incomplete and described the factors reduced the percentage yield.  In actuality, these reactions are completely done reacting but they are not 100% complete.  These reactions are reversible and exist in a state of dynamic equilibrium.

    There are several types of equilibria that a chemist could look at.  There is phase equilbria in which a substance constantly fluctuates between two states such as water vapour and condensation.  There is solubility equilbria in which a solid is constantly dissolving and precipitating.  There is redox equilibria in which ions are constantly gaining and losing electrons to exist between two states such as Fe²⁺ and Fe³⁺.  For the most part chemists deal with reaction equilibria in which the amount of reactant and products are constantly reacting back and forth regenerating each other.

    When a chemical reaction takes place in a container which prevents the entry or escape of any of the substances involved in the reaction, the quantities of these components change as some are consumed and others are formed.  Eventually this change will come to an end, after which the composition will remain unchanged as long as the system remains undisturbed. The system is then said to be in its equilibrium state, or more simply, "at equilibrium".  A chemical reaction is in equilibrium when there is no tendency for the quantities of reactants and products to change.  The direction in which we write a chemical reaction (and thus which components are considered reactants and which are products) is arbitrary because the reaction is proceeding at equal rates in both directions.  However, this does not imply that the amount of reactants and products are equal, just that they are no longer changing.

    Thus the two equations:

H₂ + I₂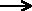 2 HI "synthesis of hydrogen iodide" 
2 HI  H₂ + I₂  "dissociation of hydrogen iodide" 

represent the same chemical reaction system in which the roles of the components are reversed, and both yield the same mixture of components when the change is completed.  This last point is central to the concept of chemical equilibrium. It makes no difference whether we start with two moles of HI or one mole each of H₂ and I₂; once the reaction has run to completion, the quantities of these two components will be the same. In general, then, we can say that the composition of a chemical reaction system will tend to change in a direction that brings it closer to its equilibrium composition. Once this equilibrium composition has been attained, no further change in the quantities of the components will occur as long as the system remains undisturbed.  Plotting data for these two reactions would then yield the same results:

    Thus a chemical equation of the form A 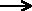 B represents the transformation of A into B, but it does not imply that all of the reactants will be converted into products, or that the reverse reaction B  A cannot also occur.  In general, both processes can be expected to occur, resulting in an equilibrium mixture containing finite amounts of all of the components of the reaction system. (We use the word components when we do not wish to distinguish between reactants and products.)  If the equilibrium state is one in which significant quantities of both reactants and products are present (as in the hydrogen iodide example given above), then the reaction is said to incomplete or reversible, but the latter term is preferable because it avoids confusion with "complete" in its other sense of being finished, implying that the reaction has run its course and is now at equilibrium.

    If it is desired to emphasize the reversibility of a reaction, the single arrow in the equation is replaced with a pair of hooked lines pointing in opposite directions, as in A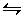B. However, there is no fundamental difference between the meanings of A  B and A B.  A reaction is said to be complete when the equilibrium composition contains no significant amount of the reactants. However, a reaction that is complete when written in one direction is said "not to occur" when written in the reverse direction.  In principle, all chemical reactions are reversible, but this reversibility may not be observable if the fraction of products in the equilibrium mixture is very small, or if the reverse reaction is kinetically inhibited (very slow.) 

    Chemical equilibrium and reaction reversibility was confirmed by many chemists, but most notably by two Norwegian chemists (and brothers-in-law) Cato Guldberg and Peter Waage.  During the period 1864-1879 they showed that an equilibrium can be approached from either direction, implying that any reaction aA + bB  cC + dD is really a competition between a "forward" and a "reverse" reaction. When a reaction is at equilibrium, the rates of these two reactions are identical, so no net (macroscopic) change is observed, although individual components are actively being transformed at the microscopic level.  Guldberg and Waage showed that the rate of the reaction in either direction is proportional to what they called the "active masses" of the various components:

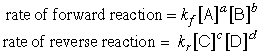
in which the proportionality constants k are called rate constants and the quantities in square brackets represent concentrations.  If we combine the two reactants A and B, the forward reaction starts immediately, but the formation of products allows the reverse process to get underway.  As the reaction proceeds, the rate of the forward reaction diminishes while that of the reverse reaction increases. Eventually the two processes are proceeding at the same rate, and the reaction is at equilibrium:

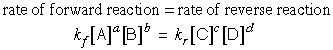
If we now change the composition of the system by adding some C or withdrawing some A (thus changing their "active masses"), the reverse rate will exceed the forward rate and a change in composition will occur until a new equilibrium composition is achieved.  This is referred to as the Law of Mass Action and is thus essentially the statement that the equilibrium composition of a reaction mixture can vary according to the quantities of components that are present. 

    How can one tell when a reaction is in a state of equilibrium?  Clearly, if we observe some change taking place a change in color, the emission of gas bubbles, the appearance of a precipitate, or the release of heat, we know the reaction is not at equilibrium.  However, the absence of any sign of change does not by itself establish that the reaction is at equilibrium, which is defined above as the lack of any tendency for change to occur; "tendency" is not a property that is directly observable! Consider, for example, the reaction representing the synthesis of water from its elements:

2 H₂ + O₂ 2 H₂O

    You can store the two gaseous reactants in the same container indefinitely without any observable change occurring. But if you create an electrical spark in the container or introduce a flame, bang!  After you pick yourself up off the floor and remove the shrapnel from what's left of your body, you will know very well that the system was not initially at equilibrium!  It happens that this particular reaction has a tremendous tendency to take place, but for reasons that we will discuss in a later chapter, nothing can happen until we "set it off" in some way- in this case by exposing the mixture to a flame, or (in a more gentle way) by introducing a platinum wire, which acts as a catalyst. A reaction of this kind is said to be highly favored thermodynamically, but inhibited kinetically.  The hydrogen iodide reaction, by contrast, is only moderately favored thermodynamically (that's why it is incomplete), but its kinetics are reasonably facile.

    It is almost always the case, however, that once a reaction actually starts, it will continue on its own until it reaches equilibrium, so if we can observe the change as it occurs and see it slow down and stop, we can be reasonably certain that the system is in equilibrium. This is by far the chemist's most common criterion.

     There is one other experimental test for equilibrium in a chemical reaction, although it is really only applicable to the kind of reactions we described above as being reversible. As we shall see later, the equilibrium state of a system is always sensitive to the temperature, and often to the pressure, so any changes in these variables, however, small, will temporarily disrupt the equilibrium, resulting in an observable change in the composition of the system as it moves toward its new equilibrium state. Similarly, addition or removal of one component of the reaction will affect the amounts of all the others. If carrying out any of these operations fails to produce an observable change, then it is likely that the reaction is kinetically inhibited and that the system is not at equilibrium.

Equilibrium State

    If a reaction is at equilibrium and we alter the conditions so as to create a new equilibrium state, then the composition of the system will tend to change until that new equilibrium state is attained. (We say "tend to change" because if the reaction is kinetically inhibited, the change may be too slow to observe or it may never take place.)  In 1884, the French chemical engineer and teacher Henri LeChâtelier (1850-1936) showed that in every such case, the new equilibrium state is one that partially reduces the effect of the change that brought it about.  This law is known to every Chemistry student as the LeChâtelier principle.  His original formulation was somewhat complicated, but a reasonably useful paraphrase of it reads as follows:  If a system at equilibrium is subjected to a change of pressure, temperature, or the number of moles of a component, there will be a tendency for a net reaction in the direction that reduces the effect of this change. 

    To see how this works, look again at the hydrogen iodide dissociation reaction:

2 HI  H₂ + I₂

    Consider an arbitrary mixture of these components at equilibrium, and assume that we inject more hydrogen gas into the container. Because the H₂ concentration now exceeds its new equilibrium value, the system is no longer in its equilibrium state, so a net reaction now ensues as the system moves to the new state.  The LeChâtelier principle states that the net reaction will be in a direction that tends to reduce the effect of the added H₂. This can occur if some of the H₂ is consumed by reacting with I₂ to form more HI; in other words, a net reaction occurs in the reverse direction. Chemists usually simply say that "the equilibrium shifts to the left". To get a better idea of how this works, carefully examine the following diagram which follows the concentrations of the three components of this reaction as they might change in time (the time scale here will typically be about an hour):

    At the left, the concentrations of the three components do not change with time because the system is at equilibrium.  We then add more hydrogen to the system, disrupting the equilibrium.  A net reaction then ensues that moves the system to a new equilibrium state (right) in which the quantity of hydrogen iodide has increased; in the process, some of the I₂ and H₂ are consumed.  Notice that the new equilibrium state contains more hydrogen than did the initial state, but not as much as was added; as the LeChâtelier principle predicts, the change we made (addition of H₂) has been partially counteracted by the "shift to the right".

    Virtually all chemical reactions are accompanied by the liberation or uptake of heat. If we regard heat as a "reactant" or "product" in an endothermic or exothermic reaction respectively, we can use the LeChâtelier principle to predict the direction in which an increase or decrease in temperature will shift the equilibrium state. Thus for the oxidation of nitrogen, an endothermic process, we can write

[heat] + N₂ + O₂ 2 NO

    Suppose this reaction is at equilibrium at some temperature T₁ and we raise the temperature to T₂.  The LeChâtelier principle tells us that a net reaction will occur in the direction that will partially counteract this change, meaning that the system must absorb some of this additional heat, and the equilibrium will shift to the right.

    Nitric oxide, the product of this reaction, is a major air pollutant which initiates a sequence of steps leading to the formation of atmospheric smog. Its formation is an unwanted side reaction which occurs when the air (which is introduced into the combustion chamber of an engine to supply oxygen) gets heated to a high temperature.  Designers of internal combustion engines now try, by various means, to limit the temperature in the combustion region, or to restrict its highest-temperature part to a small volume within the combustion chamber.

    You will recall that if the pressure of a gas is reduced, its volume will increase; pressure and volume are inversely proportional. With this in mind, suppose that the reaction

2 NO_2(g) N₂O_4(g)

is in equilibrium at some arbitrary temperature and pressure, and that we double the pressure, perhaps by compressing the mixture to a smaller volume.  From the LeChâtelier principle we know that the equilibrium state will change to one that tends to counteract the increase in pressure.  This can occur if some of the NO₂ reacts to form more of the dinitrogen tetroxide, since two moles of gas is being removed from the system for every mole of N₂O₄ formed, thereby decreasing the total volume of the system. Thus increasing the pressure will shift this equilibrium to the right.  It is important to understand that the changing the pressure will have a significant effect only on reactions in which there is a change in the number of moles of gas. For the above reaction, this change

    The volumes of solids and liquids are hardly affected by the pressure at all, so for reactions that do not involve gaseous substances, the effects of pressure changes are ordinarily negligible. Exceptions arise under conditions of very high pressure such as exist in the interior of the Earth or near the bottom of the ocean. A good example is the dissolution of calcium carbonate:

CaCO_3(s)  Ca²⁺ + CO₃^2–. 

    There is a slight decrease in the volume when this reaction takes place, so an increase in the pressure will shift the equilibrium to the right, so that calcium carbonate becomes more soluble at higher pressures.  The skeletons of several varieties of microscopic organisms that inhabit the top of the ocean are made of CaCO₃, so there is a continual rain of this substance toward the bottom of the ocean as these organisms die.  As a consequence, the floor of the Atlantic ocean is covered with a blanket of calcium carbonate. This is not true for the Pacific ocean, which is deeper; once the skeletons fall below a certain depth, the higher pressure causes them to dissolve. Some of the seamounts (undersea mountains) in the Pacific extend above the solubility boundary so that their upper parts are covered with CaCO₃ sediments.

    The effect of pressure on a reaction involving substances whose boiling points fall within the range of commonly encountered temperature will be sensitive to the states of these substances at the temperature of interest.  For reactions involving gases, only changes in the partial pressures of those gases directly involved in the reaction are important; the presence of other gases has no effect.

Equilibirum Calculations

    For the equilibrium reaction a A + b B  c C + d D , the equilibrium expression is defined as:

    In the general case in which the concentrations can have any arbitrary values (including zero), this expression is called the equilibrium quotient and its value is denoted by Q (or Qc if we wish to emphasize that the terms represent molar concentrations.)  If the terms correspond to equilibrium concentrations, then the above expression is called the equilibrium constant and its value is denoted by K (or Kc.)

    K is thus the special value that Q has when the reaction is at equilibrium.  The value of Q in relation to K serves as an index how the composition of the reaction system compares to that of the equilibrium state, and thus it indicates the direction in which any net reaction must proceed.  For example, if we combine the two reactants A and B at concentrations of 1 mol/L each, the value of Q will be indeterminately large(1÷0).  If instead our mixture consists only of the two products C and D, Q = 0. It is easy to see (by simple application of the LeChâtelier principle) that the ratio of Q/K immediately tells us whether, and in which direction, a net reaction will occur as the system moves toward its equilibrium state.  The three possibilities are:
 

Q/K	Reaction State
> 1	Product concentration too high for equilibrium; net reaction proceeds to left.
= 1	System is at equilibrium; no net change will occur.
< 1	Product concentration too low for equilibrium; net reaction proceeds to right.

    When a reaction system is not at equilibrium, the quantities of reactants or products will change until Q = K, at which point no further change will occur as long as the system remains at the same temperature and pressure. So all net change does come to an end when equilibrium is reached.  But the absence of any net change does not mean that nothing is happening!  Since all reactions are reversible at least in principal, we can regard an equilibrium A  B as the sum of two processes
 

A  B    forward reaction  rate  f = kf [A] 
B  A    reverse reaction rate    r= kr [B] 

    The expressions given in the rightmost column above simply reflect the fact that the rate at which a substance undergoes change should be proportional to its concentration; this is just another statement of the Law of Mass Action.  The proportionality constants kf and kr are the forward and reverse rate constants.  If we start with substance A alone, the absence of B means that the forward reaction alone is proceeding.  Then, as the concentration of B begins to build up, the reverse reaction comes into operation, the rate of the forward reaction diminishes due to the reduction in the concentration of B.  At some point these two processes will come into exact balance so that the forward and reverse rates are the same, at which point we can write

and combine the k’s to obtain

thus showing that the equilibrium constant can in a sense be regarded as the resultant of the two opposing rate constants. If the rate constant of the forward reaction exceeds that of the reverse step, then the equilibrium state will be one in which the product dominates. (Note carefully that although the two rate constants will generally be different, the forward and reverse rates themselves will always be identical at equilibrium.)

    The preceding paragraph shows how the concept of the equilibrium constant follows from the Law of Mass Action, but it is not a proper derivation of the formula for equilibrium constants in general.  The single most important idea for you to carry along with you from this section is that equilibrium is a dynamic process in which the forward and reverse reactions are continually opposing each other in a dead heat.

    Substances whose concentrations undergo no significant change in a chemical reaction do not appear in equilibrium constant expressions.  How can the concentration of a reactant or product not change when a reaction involving that substance takes place?  This occurs when the substance is a solid or a pure liquid phase.  This is most frequently seen in solubility equilbria, but there are many other reactions in which solids are directly involved:

CaF_2(s) Ca²⁺_(aq) + 2 F^–_(aq)

Fe₃O_4(s) + 4 H_2(g) 4 H₂O_(g) + 3 Fe_(s)

    These are heterogeneous reactions (meaning reactions in which some components are in different phases), and the argument here is that concentration is only meaningful when applied to a substance within a single phase.  Thus the term [CaF₂] would refer to the “concentration of calcium fluoride within the solid CaF₂, which is a constant depending on the molar mass of CaF₂ and the density of that solid.  The concentrations of the two ions will be independent of the quantity of solid CaF₂ in contact with the water; in other words, the system can be in equilibrium as long as any CaF₂ at all is present.

    Your ability to interpret the numerical value of a quantity in terms of what it means in a practical sense is an essential part of developing a working understanding of Chemistry.  This is particularly the case for equilibrium constants, whose values span the entire range of the positive numbers.  Although there is no explicit rule, for most practical purposes you can say that equilibrium constants within the range of roughly 0.01 to 100 indicate that a chemically significant amount of all components of the reaction system will be present in an equilibrium mixture and that the reaction will be incomplete or “reversible”.  As an equilibrium constant approaches the limits of zero or infinity, the reaction can be increasingly characterized as a one-way process; we say it is “complete” or “irreversible”. T he latter term must of course not be taken literally; the LeChâtelier principle still applies (especially insofar as temperature is concerned), but addition or removal of reactants or products will have less effect.  Although it is by no means a general rule, it frequently happens that reactions having very large or very small equilibrium constants are kinetically hindered, often to the extent that the reaction essentially does not take place.

    Equilibrium expressions can be mathematically calculated to have units, yet these quantities are often represented as being dimensionless.  For the most part, we do not worry about the units for the equilibrium constant even though in some cases this information may be relevant.  Strictly speaking, equilibrium expressions do not have units because the concentration or pressure terms that go into them are really ratios in which the unit quantity in the denominator refers to the standard state of the substance; thus the units always cancel out.  For substances that are liquids or solids, the standard state is just the concentration of the substance within the liquid or solid, so for something like CaF_2(s), the term going into the equilibrium expression is [CaF₂]/[CaF₂] which cancels to unity; this is the reason we don't need to include terms for solid or liquid phases in equilibrium expressions. The subject of standard states would take us somewhat beyond where we need to be at this point in the course, so we will simply say that the concept is made necessary by the fact that energy, which ultimately governs chemical change, is always relative to some arbitrarily defined zero value which, for chemical substances, is the standard state.

    To actually calculate the equilibrium constant, one must know the concentration or pressure of the relative species involved in the reaction.  Once this has been determined, mere substitution in the equilibrium expression will yield the value of K at that temperatue.  If the temperature changes, the value of K will change and this value is only accurate providing the reaction is truly at equilibrium.

• Consider the following equilibrium:  H_2(g) + I_2(g) 2 HI_(g) such that at equilibrium the concentration of  each reactant is 0.1 M and the concentration of the product is 0.4 M.  Calculate the value of the equilibrium constant at this temperature.

K = [HI]²/[H₂]_[I₂]  =  0.4²/(0.1)(0.1) = 16

    Typically, one does not know the equilibrium concentrations, but knows the starting amounts and the equilibrium constant.  In which case, let x = the amount of change in concentration that occurs while the reaction works to achieve equilibrium.

• Consider the following equilibrium:  H_2(g) + I_2(g) 2 HI_(g) .  Equal amounts (0.100 M each) is introduced to a 1 L container, and then the temperature is raised to 731 K.  Calculate the concentration of each species when the system is at equilibrium if K = 50.3.

For convenience, we write down the reaction equation and put the concentration of the species below the formula in a chart. 
 

                         H_2(g) +     I_2(g) 2 HI_(g)

Initial (I)	0.1	0.1	0
Change (C)	-x (loss)	-x	+ 2x (gain)
Equilibrium (E)	0.1 - x	0.1 - x	2x

K = 50.3 = [HI]²/[H₂]_[I₂]  = (2x)²/(0.1 - x)(0.1 - x)

50.3 = 4x²/(0.01 - 0.2x + x²)

Expanding the above equation gives, 46.3 x² - 10.6x + 0.503 = 0.

Solving this quadratic yields x = 0.139 and 0.078, but only 0.078 is relevant since x cannot be larger than the starting amounts and thus we have: 

[H₂] = [I₂] = 0.100 - 0.078 = 0.022 M
[HI] = 2x = 0.156 M

It is always a good idea to check the validity of the answer. We use the result to calculate the equilibrium constant. 
0.0243/0.0.000484 = 50.3 = K.