Numbers
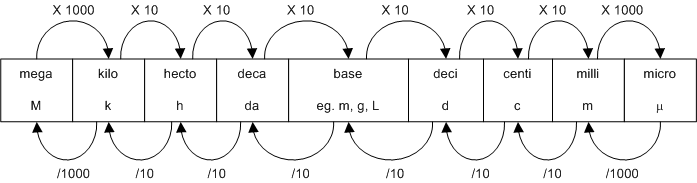
To be able to use quantitative physical properties, it is important to be fluent with the metric system. The following is a table of the most common prefixes:
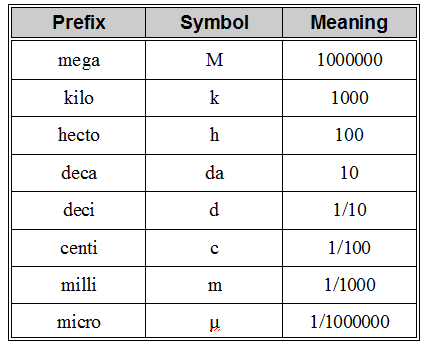
The following figure is useful for metric conversions:
Typicall scientific numbers are so large and require high levels of precision. As a result, scientific notation is often used. The rules are
Rules for Scientific Notation
- non-zero digit is placed before the decimal
- about 2-5 digits are placed after the decimal
- "X 10" to the appropriate exponent is placed after the number--if you have to move the decimal to left, exponent is more
positive and if you move decimal to right, exponent is more negative
e.g. express the following numbers in scientific notation:
- 1994 = 1.994 X 103
- 0.051 = 5.1 X 10-2
- 6.75 = 6.75 not 6.75 X 100as 100 is always omitted
Note that the EXP button on calculator = "X 10" thus hit EXP before typing the exponent (if you don't have a calculator, convert all numbers to same
exponent and subtract exponents if dividing, add exponents if multiplying or keep same exponent if adding/subtracting).
Atomic Theory
The investigation of atomic theory began with Leucippus of Miletus and his student Democritus of Abdera (5th Century BC). They stated that all matter is made up indivisible particles called atoms and there is a void, which is empty space between atoms. Atoms are completely solid and are homogenous, with no internal structure. Atoms vary in size, shape and weight. Atoms possessed characteristics of the matter in which they were found; thus, wood atoms differ from diamond atoms. In the 4th century (BC), atomic theory was considered blasphemy because there is no finite quality to the universe as it was created by an outside power. This was supported by Aristotle and as a result atomic theory was abandoned.
In 1803, John Dalton stated that he agreed with the ancient Greek philosophers. He proposed an atomic theory which was based upon
measurable properties of such as mass. His theory of the atom conserved the inferences that the atom was an
undefined solid, was indivisible and measurable (mass), but introduced the idea that the atom was a sphere and
matter’s properties were defined by its atoms (not vice versa).
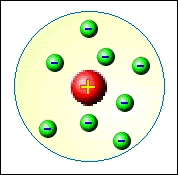
In 1897, J.J. Thomson theorized that atoms were indeed spherical, indivisible and
possessed a unique mass; however, based on research, he concluded that each atom has an unique internal
structure of a positive field with negatives embedded within its matrix.
In 1911, Niels Bohr earned his PhD in Denmark with a dissertation on the
electron theory of metals. Right afterward, he went to England to study
with J.J. Thomson, who had discovered the electron in 1897. Most
physicists in the early years of the twentieth century were engrossed by
the electron, such a new and fascinating discovery. Few concerned
themselves much with the work of Max Planck or Albert Einstein. Thomson
wasn't that interested in these new ideas, but Bohr had an open mind.
Bohr
soon went to visit Ernest Rutherford (a former student of Thomson's) in
another part of England, where Rutherford had made a brand-new discovery
about the atom.
Rutherford's
findings came from a very strange experience. Everyone at that time imagined
the atom as a "plum pudding." That is, it was roughly the same consistency
throughout, with negatively-charged electrons scattered about in it like
raisins in a pudding. As part of an experiment with x-rays in 1909,
Rutherford was shooting a beam of alpha particles (or alpha rays, emitted
by the radioactive element radium) at a sheet of gold foil only 1/3000
of an inch thick, and tracing the particles' paths. Most of the particles
went right through the foil, which would be expected if the atoms in the
gold were like a plum pudding. But every now and then, a particle
bounced back as though it had hit something solid. After tracing
many particles and examining the patterns, Rutherford deduced that the
atom must have nearly all its mass, and positive charge, in a central nucleus
about 10,000 times smaller than the atom itself. All of the negative
charge was held in the electrons, which must orbit the dense nucleus like
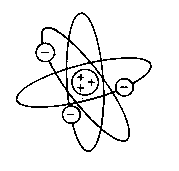
planets around the sun. His model had the following postulates:
- An atom consists of a central nucleus. This
nucleus is composed of positively charged protons, and electrically uncharged
(neutral) neutrons.
- Negatively charged electrons revolve round the nucleus
in definite orbits.
- The orbits themselves can be at any distance from
the nucleus.
- In any atom, the number of protons is equal to the
number of electrons, and hence it is electrically neutral.
This was the birth of the nuclear atom.
The Mole
Lorenzo Romano Amedeo Carlo Avogadro, conte di Quaregna e di Cerreto (1776
- 1856), was born in Turin, Italy, on 9th August, 1776. In spite
of a successful legal career, Avogadro also showed an interest in natural
philosophy, and in 1800 he began private studies of mathematics and physics.
In 1809 became professor of natural philosophy at the college of Vercelli.
In 1811, Avogadro published an article in Journal de physique that clearly
drew the distinction between the molecule and the atom. He pointed
out that Dalton had confused the concepts of atoms and molecules.
Dalton still equated particles with atoms, and could not accept how one
particle of oxygen could yield two particles of water. The "atoms"
of nitrogen and oxygen are in reality "molecules" containing two atoms
each. Thus two molecules of hydrogen can combine with one molecule of oxygen
to produce two molecules of water. Avogadro suggested that equal
volumes of all gases at the same temperature and pressure contain the same
number of molecules
which is now known as Avogadro's Principle. It was long after
Avogadro that the idea of a mole was introduced. Since a molecular weight
in grams (mole) of any substance contains the same number of molecules,
then according to Avogadro's Principle, the molar volumes of all gases
should be the same. The number of molecules in one mole is now called
Avogadro's number. It must be emphasized that Avogadro, of course, had
no knowledge of moles, or of the number that was to bear his name. Thus
the number was never actually determined by Avogadro himself. It
is a honourary accreditation to all his work.
As we all know today, Avogadro's number is very large, the presently accepted
value being 6.0221367 x 1023. The size of such a number is extremely
difficult to comprehend. There are many awe-inspiring illustrations to
help visualize the enormous size of this number. For example: An
Avogadro's number of standard soft drink cans would cover the surface of
the earth to a depth of over 200 miles. If you had Avogadro's number
of unpopped popcorn kernels, and spread them across the United States of
America, the country would be covered in popcorn to a depth of over 9 miles.
If we were able to count atoms at the rate of 10 million per second, it
would take about 2 billion years to count the atoms in one mole.
Cannizarro, around 1860, used Avogadro's ideas to
obtain a set of atomic weights, based upon oxygen having an atomic weight
of 16. In 1865, Loschmidt used a combination of liquid density, gaseous
viscosity, and the kinetic theory of gases, to establish roughly the size
of molecules, and hence the number of molecules in 1 cm3 of
gas. During the latter part of the nineteenth century, it was possible
to obtain reasonable estimates for Avogadro's number from sedimentation
measurements of colloidal particles. Into the twentieth century, then Mullikens
oil drop experiment gave much better values, and was used for many years.
A more modern method is to calculate the Avogadro number from the density
of a crystal, the relative atomic mass, and the unit cell length, determined
from x-ray methods. To be useful for this purpose, the crystal must be
free of defects. Very accurate values of these quantities for silicon have
been measured at the National Institute for Standards and Technology (NIST).
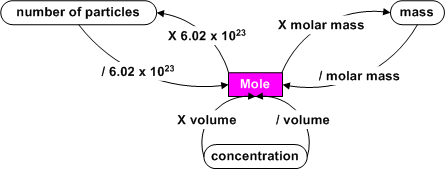
Mole Math
When you know how many moles of a substance you have, you can calculate the number of atoms present since 1 mole = 6.02 x 1023 particles of the substance. For example, there are 2 moles of oxygen for every 1 mole of CO2 , so there are 2 X 6.02 x 1023 = 1.20 x 1024 atoms of oxygen present. If there were only 0.30 moles of CO2 , there would be 2 (atoms/molecule) X 0.30 (moles) X 6.02 x 1023 (molecules/mole) = 3.6 x 1023 atoms of oxygen.
We also know that we can find
the mass of a sample by using a balance in the laboratory. By dividing
the mass of a sample by its molar mass (taken from the periodic table), we get the number of moles of the
substance.
Example 1.
If you find the mass of a sample of glucose (C6H12O6)
to be 90.0 g, how many moles of glucose do you have? We look up the
masses of each atom on the periodic table, multiply by the number of atoms
present and add the total.
Molar mass of C6H12O6 is:
Carbon = 12.0 g x 6 atoms = 72.0 g
Hydrogen = 1.01 g x 12 atoms = 12.1 g
Oxygen = 16.0 x 6 atoms
= 96.0 g
---------
180.1 g
Now use the formula:
mol = 90.0 g/180 g/mol = 0.500 mol
Example 2.
A certain laboratory procedure requires the use of 0.100 moles
of magnesium. How many grams of magnesium would you mass out on the
balance?
From the period table we get the Molar mass of magnesium as 24.3 g.
Now rearrange the formula:
mass = (mol)(molar mass) = (0.100 mol)(24.3
g/mol) = 2.43 g of magnesium
Example 3.
How many molecules of carbon dioxide are found in 2.50 moles of carbon
dioxide?
Here we recall that:
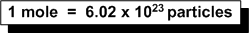
Set up a ratio:
1 mole = 6.02 x 1023 molecules/mol
2.50 mol = x molecules of CO2
Solve by rearranging:
x molecules of CO2 = (2.50 mol)(6.02 x 1023
molecules/mol) = 1.51 x 1024 molecules of CO2
Example 4.
How many moles are represented by 7.45 x 1024 molecules of
O2?
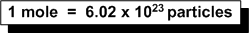
Set up a ratio:
1 mole = 6.02 x 1023 molecules/mol
x mol = 7.45 x 1024 molecules of O2
Solve by rearranging:
x moles = (1) (7.45 x 1024 molecules)/6.02 x 1023
molecules/mol = 12.4 moles of O2
Also, 1 mole of any gas at STP (P = 101.3 kPa or 760 torr or 1 atm and T = 273 K) occupies 22.4 L. At SATP (T = 298 K and P = 100 kPa), this volume becomes 24.8 L. For example if we have 11 L of He at STP, we have 11/22.4 or 0.49 moles of He gas. Another way to express amount of solute that a solution can contain is by stating the amount of moles of solute present in 1 L of solution and this is called molarity. Molarity = moles of solute/ L of solution or M = n/V. To dilute a solution you add more solvent to it resulting in the following relationship: M1V1 = M2V2. You may need to convert between units such as number of particles
to mass. This can be done by first converting to moles or by working
with molar equivalents.
Stoichiometry
The word stoichiometry derives from two Greek words:
stoicheion (meaning "element") and metron (meaning "measure"). Stoichiometry
deals with calculations about the masses (sometimes volumes) of reactants
and products involved in a chemical reaction.
Consider an equation:
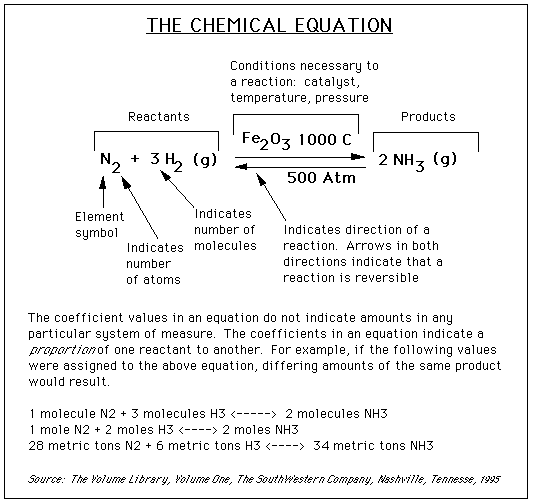
To work with chemical equations and reactions, the equations must first be balanced. To do this numerical coefficients are placed in front of chemical formulas in equations as per the following guidelines:
- balance the element (other than hydrogen or oxygen) that has greatest number of atoms in any reactant or product
- balance other elements (other than hydrogen or oxygen)
- balance oxygen or hydrogen, whichever is present in the combined state and leave until last whichever is present in
uncombined state (ie. elemental state: H2 or O2)
- check the equation by counting the number of atoms of each element on each side of the equation
- get rid of all fractions and reduce all coefficients to lowest terms
Example 1.
Given the Haber Process: N2 + 3 H2
2 NH3 Determine the grams of H2 that
will react with the 4 moles of N2.
Convert moles of N2 given to moles of requested H2.
This requires the use of the coefficients of N2 and H2
from the balanced equation:
N2 + 3 H2
2 NH3
Set up the ratios:
1 mole N2 = 3 moles H2
4 moles N2 = x moles H2
Solve by rearranging:
(1 mole of N2)(x moles of H2) = (4 moles of
N2)(3 moles of H2) = 12 moles of H2
Convert the moles of requested H2 to grams of H2
using:
12 mole H2 = x grams H2/2.0 grams of H2
Solve by rearranging:
x grams of H2 = (12 moles H2)(2.0 grams
H2) = 24.0 grams H2
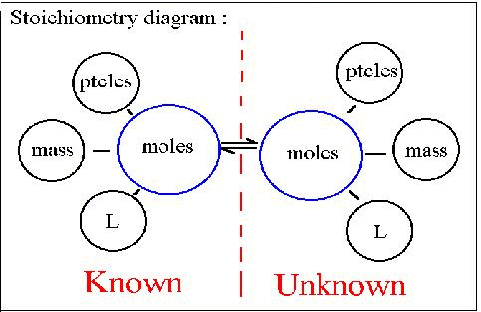
Sometimes the reactants for a reaction in an experiment
are not necessarily a stoichiometric mixture. In a chemical reaction, reactants
that are not use up when the reaction is finished are called excess reagents.
The reagent that is completely used up or reacted is called the limiting
reagent, because its quantity limit the amount of products formed.
Consider the reaction between sodium and chlorine. The reaction can be
represented by the equation:
2 Na + Cl2
2 NaCl
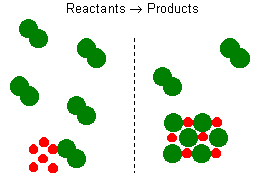This balanced reaction equation indicates that two Na atoms would react
with two Cl atoms or one Cl2 molecule. Thus, if you have 6 Na
atoms, 3 Cl2 molecules will be required. If there is an excess
number of Cl2 molecules, they will remain unreacted. We can
also state that 6 moles of sodium will require 3 moles of Cl2
gas. If there are more than 3 moles of Cl2 gas, some will remain
as an excess reagent, and the sodium is a limiting reagent. It limits the
amount of the product that can be formed. To solve these types of
questions you can either use one reactant at a time to determine which
reactant produces the least amount of product. This will represent
the correct answer and the reactant use will represent the limiting reagent.
Alternatively, you can calculate the molar ratio of each reactant by finding
the moles of each reactant and dividing by the respective numerical coefficients
from the balanced equation. The reactant with the smaller molar amount
limits the reaction and should be used for all future calculations.
Net Ionic Equations
The presence of a driving force for reactions done
in water can be evaluated using a net ionic equation. The total and net
ionic equations show the real physical state of every component of the
reaction. The compound is a strong electrolyte (a soluble ionic compound
or a strong acid), then the compound is separated into the appropriate
aqueous ions. Otherwise it is left in an undisassociated (ionic compounds)
state or un-ionized state (weak acids, bases and water).
Example 1: CaCO3(s) + HCl
?
Molecular Equation: CaCO3(s) + 2 HCl(aq)
CaCl2(aq) + H2O(l) + CO2(g)
Total Ionic Equation:
CaCO3(s) + 2 H+(aq) + 2Cl-(aq)
Ca2+(aq) + 2 Cl-(aq) + H2O(l)
+ CO2(g)
Net Ionic Equation:
CaCO3(s) + 2 H+(aq)
Ca2+(aq) + H2O(l) + CO2(g)
The driving force was the formation of water and gas!
Example 2: Fe(s) + AgNO3(aq)
?
Molecular Equation:
Fe(s) + 2 AgNO3(aq)
2 Ag(s) + Fe(NO3)2(aq)
Total Ionic Equation:
Fe(s) + 2 Ag+(aq) + 2 NO3-(aq)
2 Ag(s) + Fe2+(aq) + 2 NO3-(aq)
Net Ionic Equation:
Fe(s) + 2 Ag+(aq)
2 Ag(s) + Fe2+(aq)
The driving force was the transfer of electrons from
iron (the reducing agent) to the silver ion (the oxidizing agent). Remember:
The reducing agent is the reactant that donates the electrons to the reactant
that is reduced. When the reducing agent loses electrons, it is oxidized.
The oxidizing agent in the reactant that receives the electrons from the
reactant that is oxidized. In doing so, the oxidizer is reduced.
Example 3: K3PO4(aq) + 3 HNO3(aq)
?
Molecular Equation: K3PO4(aq) + 3 HNO3(aq)
H3PO4(aq) + 3 KNO3(aq)
Total Ionic Equation:
3 K+(aq) + PO43-(aq)
+ 3 H+(aq) + 3 NO3-(aq)
H3PO4(aq) + 3 K+(aq) + 3 NO3-(aq)
Net Ionic Equation: PO43-(aq) + 3 H+(aq)
H3PO4(aq)
The driving force was the formation of the weakly ionized acid.
Example 4: KNO3(aq) + HCl(aq)
?
Molecular Equation: KNO3(aq) + HCl(aq)
KCl(aq) + HNO3(aq)
Total Ionic Equation:
K+(aq) + NO3-(aq) + H+(aq)+
Cl-(aq)
K+(aq) + Cl-(aq) + H+(aq)
+ NO3-(aq)
Net Ionic Equation: There is no net because all species remained
as aqueous ions before and after; therefore, there is no reaction.
Significant Digits
Significant figures are digits that are statistically
important or valuable. There are two kinds of values in science
and hence two different ways to identify the proper number of
significant figures.
1. Measured Values
The key issue here is that the number of significant
digits is determined by the precision of the measuring device used.
In every case measurements include one level of estimation. That
is the last number reported in a measurement is an educated guess using
the scale provided by the measuring device. Consider a ruler which
is calibrated in centimeters. Therefore, between each cm marking there
will be ten unnumbered calibration marks. This estimated number is the
last significant digit presented in the measurement.
2. Computed Values
Rules have been developed to ensure that error due
to estimation is minimized during all calculations.
Rules for Determining the Number of Significant Digits In Numbers With
Indicated Decimals
- All non-zero digits (1-9) are to be counted as significant.
-
Zeros that have any non-zero digits anywhere to the LEFT of them are considered
significant zeros.
- All other zeros not covered in rule 2 above are NOT to be considered significant
digits.
E.g. 1. 0.0040000
The 4 is significant (Rule 1) and the first three
zeros are not significant (Rule 3), but the last four zeros are significant
(Rule 2). Therefore the number has a total of five significant digits.
E.g. 2. 120.00420
The digits 1, 2, 4, and 2 are significant (Rule 1)
and all zeros are considered significant (Rule 2). So there are a total
of eight significant digits.
Some difficulty arises when a number does not have
a decimal place. For example, consider 1,000,000 where is it not
apparent that any estimation is included in the number or how precise the
measurement really was. If the number is written as 1,000,000. then the
decimal place tells us that there are 7 significant digits as the decimal
indicates the level of precision. If there is no decimal then only
the 1 may be confidently reported as significant. In reality this
case evokes the use of an arbitrary rule of 3 or 4 significant place holders
is employed and such a number is written in scientific notation as 1.00
X 106. In scientific notation all the numbers are significant
which is another reason they are often used in science.
During multiplication/division the answer must have
the same number of significant digits as the number in the computation
with the least number of significant digits.
E.g. 3. (0.000170)(100.40) = 0.0171 since the answer can only have 3
significant digits.
E.g. 4. (2.000 X 104 )/(6.0 X 10-3) = 3333333.333
but the answer can only have 2 significant digits so this number must be
converted to scientific notation to properly express the answer (3.3 x
106).
For addition/subtraction, the focus shifts from significant
digits to number of decimal places because the answer can not be more precise
than the least precise number used in the calculation. Therefore,
the answer will only have the same number of decimal places as the number
with the least number of decimal places in the calculation.
E.g. 5. 160.45 + 6.732 = 167.18 since 160.45 is the least precise.
In all cases it is important to keep all the numbers
involved in a calculation until the very end to ensure proper rounding
of the answer. Typically, if the last digit used for rounding is
a 5 followed by no other digits, round down. For example 4.565 rounded
to three significant digits becomes 4.56. However, in this course
we are not going to worry about being so precise.
R. H. Logan, Instructor of Chemistry, Dallas County Community College
District, North Lake College.
