Evolution of Atomic Theory

   Over time, understanding of atomic structure has evolved because until recently scientists could only infer internal structure because it was not possible to actually see inside an atom and so they had to apply some sort tool to alter atoms and then measure the observable outcome to deduce internal composition. These tools must be able to work on the internal structure so they must be same magnitude–light, energy, radiation, etc. which means the tools themselves were quite specific and sophisticated. As these tools became more elaborate, it creates the illusion that the atom itself has evolved over time because wondrous new insights seem to just be created, but clearly it is only our understanding and interpretation of atomic structure that has changed over time. This is further complicated by the fact that over time anomalies accumulate which cannot be simply ignored and must be rationalized by reconciling a previous model making the data collected appear more convoluted. The scientists that make sense of this data are often shocked by their own interpretations and it takes considerable time to verify their ideas to ultimately be accepted or rejected.

   Further complicating the issue is the need to represent atoms in some manner. Typically this is done with models; however, models have limitations which interfere with full understanding for the average person. These limitations are not errors in terms of wrong information or data, but rather short-comings due to the nature of models themselves. That is, the models need to oversimplify things to make them easier to understand which makes gross over-assumptions, are static even though atoms are in flux and have motion, exaggerate size–comparisons and distance–multiple scales often used to fit everything, are often two-dimensional representations of three-dimensional aspects, describe interacting components which implies constant change which cannot be shown, can deal with duality (such as wave/particle) even though only one aspect can be shown at one time and some atomic aspects really cannot be fully measured like electrons or properly be represented in every model.

Democritus (400 B.C)

   He observed that no matter how small something was made, it retained its properties which led him to infer that matter is made up indivisible particles or atomos (indestructible components) which resembled the original matter both internally and externally. This means that atoms retain the properties of the original matter from which the were studied. For example, water is wet, water atoms are wet (yes, water is not an atom, but this was before any periodic table had been conceived). Iron atoms rusted and etc. However, even Democritus knew this was a problem because you don't have to eat hair or meat to grow new hair of meat, which means matter changes from one atom type to another. Unfortunately, society didn't like these horrifying ideas and upon threat of death, Democritus decided to pursue other avenues of learning.

Dalton (1803)

   Surprisingly, the next major breakthrough took a considerable amount of time to develop and it would rectify Democritus's dilemma Dalton continued with the theory that atomic structure is defined by unique and measurable characteristics (for example, mass) similar to Democritus, but he also introduced the idea that the atom was a sphere and matter’s properties were defined by its atoms (not vice versa according to Democritus). This allowed atoms to be reconstructed using the same atoms and a sphere makes sense since this is the most indestructible shape. The sphere also makes sense since an atom's interactions is the same in all directions. However, despite inferring atoms must have an internal structure to evoke properties and interactions, there was no way to determine the nature of this internal structure. The quest to solve this puzzle had started and this was the beginning of the atomic age.

Crookes (1879)

   Now there was much more rapid change as technology is developing quickly. Crookes experimented with applying an electric discharge (generated with a hand-crank) to one end of a partially evacuated gas tube. The partial vacuum allowed for lower electrical resistance and if the tube was completely evacuated, it was empty and no electricity could travel so something needs to be in the tube. The gas tubes were coated with zinc sulfide dust because it glows when stimulated by energy. He found that there were glowing rays moving away from the electrical discharge and later these rays were called cathode rays since they moved away from the cathode which is the end that was electrocuted.

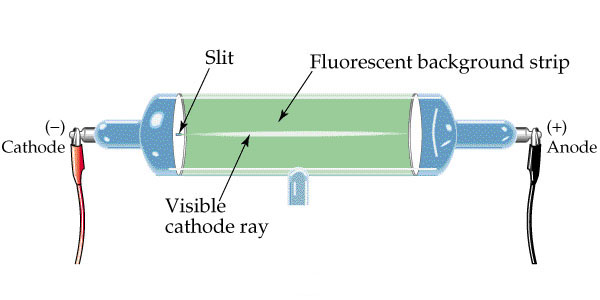
   Crookes went on to analyze these newly discovered rays. These cathode rays indicated that something was moving quickly through the tube. He also found that if he put charged plate with the identical type of charge as the discharge next to the body of the glass tube, the glowing rays moved away from the charged plate. This charge was later found to be negative (after his work). He also found that the cathode rays would bend toward an oppositely charged or positive plate. Despite the bending effects, some argued that it was just light energy.

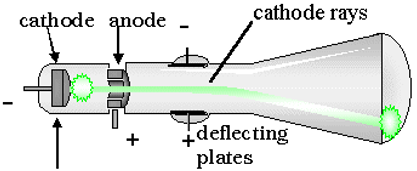
   Crookes was convinced that it was not just light and devised a way to prove it. He found that the glowing rays could push a small pinwheel up hill inside one of these Crookes’ tubes.

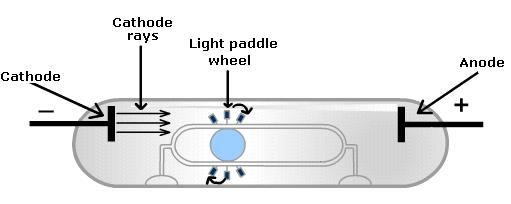
   He theorized that some almost massless, negatively charged component was being hurled out of the atom through the tube and the first sub-atomicparticle had been found.

Goldstein (1886)

    Goldstein modified the Crookes’ tubes by bending them and applying the electrical discharge in the middle of the tube. He found glowing rays called canal rays moving very slowly in the opposite direction from the cathode rays. He also found that canal rays would bend away from what was later found to be a positively charged plate and toward what was later determined to be a negatively charged plate. Initially, it was thought that this was releasing another subatomic particle from the atom but it was soon realized that since these new "subatomic particles" moved very slowly, they were more massive (i.e. had more mass) and meant that once cathode ray particles are removed the rest of the atom is positively charged. However, this still proves that the atom does contain another subatomic particle since there is also a positively charged component.

Thomson (1897)

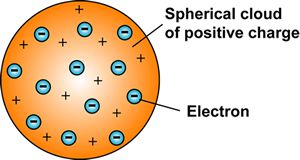
    Thomson was working with these other scientists conducting research as well. However, he is more noted here for using all these observations to theorize an atomic model comprising sub-atomic structure. He used all these new observations to infer that the atom was spherical, indivisible and possessed a unique mass however, based on research, he concluded that each atom has an unique internal structure of a positive field with negatives embedded within its matrix. He called the negatives corpuscles because the term electron had not been used yet. We know have what is considered the first structured atomic model which provided direction for all subsequent research.

Rutherford (1911)

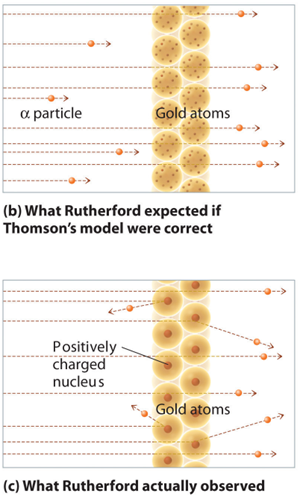
    Rutherford conducted an experiment which definitely changed the Thomson model. Rutherford used a very small tool to probe the internal structure of atoms; he used alpha radiation as it could interact with the small components of the atom. He bombarded thin gold sheets with beams of the radiation and surrounded the gold foil with a zinc sulfide coated plate which would become excited when hit by the alpha radiation. He found that most of the alpha radiation passed straight through which supported Thomson’s model which had the mass of the atom so spread out it would not be dense enough to block the alpha radiation. However occasionally, Rutherford found that the alpha rays deflected off at angles and this contradicted Thomson’s model.

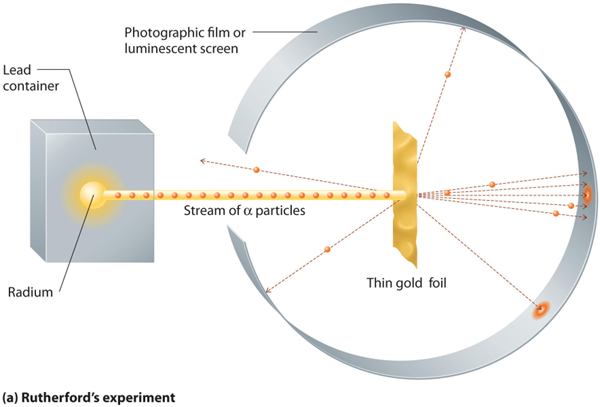
    These new findings required a subtle but important change to the current atomic theory. Based on these new observations, the atom could not be a solid positive mass as Thomson predicted, but rather, the atom must have all the positive mass localized in the center of the atom which deflects the alpha particles when they hit here because the mass is so densely packed. Remember, we know the positive area has mass, because this portion of the atom moves slowly when excited. And the almost massless negative charges must be orbit the nucleus roaming in an empty space which continues to allow alpha particles to pass through. If the atom was all dense mass, alpha particles would never pass through.

Chadwick (1932)

    Chadwick was working with Rutherford’s experiment but a fortuitous change in the set up led to an interesting new result. He used beryllium foil in place of the gold foil which obviously has slightly different atomic properties. He found that after alpha bombardment, a brand new slow-moving ray was occasionally detected. The actual method of detection is quite complex but in the end it was found that this this new ray did not make the plate glow and it resulted in the deterioration of the foil over time which is new as Rutherford’s work did not affect the gold foil. This means that this new experiment damaged the atoms in some way. Chadwick also found that this ray did not alter its path by nearby positively or negatively charged plates. It was believed that Chadwick had knocked a neutral sub-atomic particle out of some locked in place within the atom; that being the nucleus. So yes, this is the first nuclear reaction created on purpose in a lab.

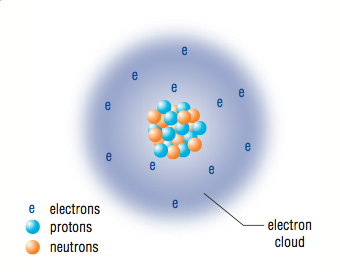
    Now there is enough evidence to force scientists to modify the Thomson atom. The result is called the Nuclear atom. So we now know that the atom is largely made up of empty space through which the essentially massless negative electrons travel around the dense centrally located nucleus made up of positively charged protons and neutrally charged neutrons. The electrons are held around the nucleus due to their attraction to the oppositely charged protons. Finally, the mass of the entire atom is confined to the nucleus because that is where the protons and neutrons are found.

Moseley (1913)

    Moseley worked at the same time as Rutherford following up Rutherford’s work on protons in the nucleus. He bombarded nuclei of different atoms using single beams of x-rays. The beams were created by passing them through thin slits and the atoms were exposed in thin crystals of pure elements. He observed a diffraction pattern exposing a photographic film representing a change in the pathway or wavelength due to small changes in the energy of the x-rays. This was due to colliding with protons which absorbed some of the energy. He then used the degree of x-ray bending to determine the number of proton collisions which indicated the number of protons present in the nucleus.

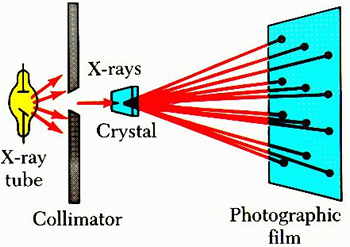
    Basically, x-rays are deflected by protons and each proton hit within an atom of the sample adds to the angle of deflection. In the end, he was able to precisely determine the amount of x-ray bending per proton number present in a sample of the element which then showed that each element has a unique number of protons due to a unique amount of bending. This led to the determination of the exact number of protons present in an atom of an element which is now called the atomic number and the symbol is capital Z. This is often written as a subscript in front of the element symbol.

Soddy (1913)

    Soddy worked at McGill in Montreal with Rutherford on Rutherford’s experiments. Soddy later went on to make the next important clarification of atomic structure. He initially noticed that a change in 1 proton between elements did not always result in the predicted linear change in mass. Something was missing. He then worked with radioactive elements that decayed into the same element. He found that even though proton numbers remained constant, there was still a change in mass.

    Thus, since neutrons represent the other particle with mass in the nucleus, the number of neutrons must be able to independently change as this would account for the change in mass. Soddy went on to win a Nobel prize for these findings and subsequent conclusions: atoms with the same proton number remain the same element but if they have a different number of neutrons and hence mass, they are specifically called isotopes. The number of protons plus neutrons is called the mass number and the symbol is capital A. This is called the mass number since these sub-atomic particles are responsible for almost all of the mass of the atom. However, the mass number is not the mass of the atom. The mass number is shown as a superscript before the symbol of the element. So all of this information is shown as indicated by the diagram.

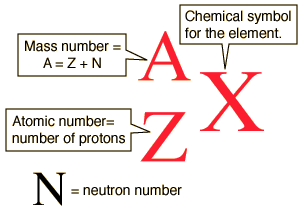
    Consider the 3 isotopes of hydrogen which are given specific names. Notice how the A-Z number relate to the atomic structure. The first most common isotope of hydrogen is sometimes also called protium.

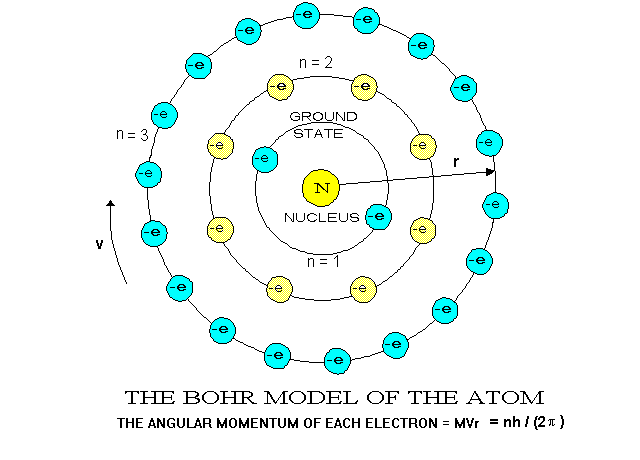
The Bohr-Rutherford Atom (1913)

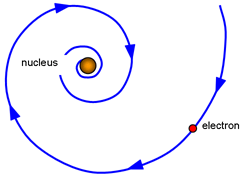
    Extensive study of the nuclear model raised some concerns. In fact Rutherford acknowledged that the model needed revision as he worked to develop this model. By all rules of classical physics, it should be very unstable. Over time, 3 key limitations (not errors) were noted. The first limitation deals with electron motion. Electrons use energy to move which means they should lose energy over time so what prevents them from eventually slowing enough to collapse into the nucleus due to attraction to the positive protons. 

    The second key limitation also relates to electron motion, but more due to distance from the nucleus. Some electrons eventually sit far from the nucleus due to random motion so what prevents theses outer electrons from overcoming the attractive pull of the nucleus and escaping the atom on their own or the electrons could be knocked out of position if a charged particle passed by. 

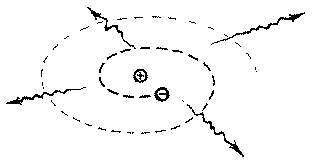
    Finally, the third key limitation, which although scientists did not fully understand, they did learn how to put it to use. The basic law of electrostatic charges states that like charges repel and positive protons are tightly confined to the incredibly small space of the nucleus so what force is overcoming this immense force of repulsion to keep the nucleus together.

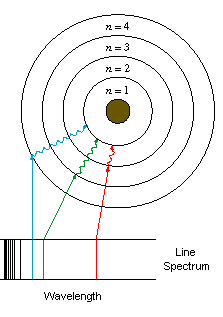
    Furthermore, Rutherford's description of the atom could not be entirely correct because it did not account for some observations that had already been made.  Perhaps the most important of these observations concerned the behaviour of certain gases.  These gases at low pressure emit light in a set of discrete bands of the electromagnetic spectrum (see below).  This is quite different from the radiation emitted by solids, which is spread evenly across the electromagnetic spectrum (see below).  The radiation emissions of these gases were important because they showed that at least under some circumstances, the orbits of the electrons could not be at just any distance from the nucleus, but were confined to discrete distances (or energy states). 

    Bohr turned to Planck's quantum theory to explain the stability of most atoms.  He found that the ratio of energy in electrons and the frequency of their orbits around the nucleus was equal to Planck's constant (the proportion of light's energy to its wave frequency, or approximately 6.626 x 10^-23 ).  Bohr suggested the revolutionary idea that electrons "jump" between energy levels (orbits) in a quantum fashion, that is, without ever existing in an in-between state.  Thus when an atom absorbs or gives off energy (as in light or heat), the electron jumps to higher or lower orbits.  Bohr published these ideas in 1913 to mixed reaction.  Many people still hadn't accepted the idea of quanta, or they found other flaws in the theory because Bohr had based it on very simple atoms. But there was good evidence he was right: the electrons in his model lined up with the regular patterns (spectral series) of light emitted by real hydrogen atoms. 

    Bohr's theory that electrons existed in set orbits around the nucleus was the key to the periodic repetition of properties of the elements.  The shells in which electrons orbit have different quantum numbers and hold only certain numbers of electrons -- the first shell holds no more than 2, the second shell up to 8, the third 18, the fourth 14.  Atoms with less than the maximum number in their outer shells are less stable than those with "full" outer shells.  Elements that have the same number of electrons in their outermost shells appear in the same column in the periodic table of elements and tend to have similar chemical properties. 

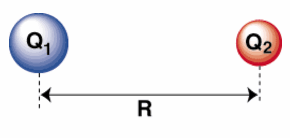
Coulomb's Law

    Periodic trends can be verified mathematically (in fact they were initially proven mathematically).  One simple method that uses approximations to verify periodic trends is to apply Coulomb's law of attraction.  This law is often apply on a macroscopic scale to define the attractive force between two objects. Thus, it can be applied to gravitational forces between two stellar objects.  However, the same rules of physics must apply on a microscopic level as well; therefore, we can apply it to the force of attraction between protons and electrons within an single atom.  Coulomb's Law states that the electrostatic force between two charged objects is directly proportional to the product of the charges and inversely proportional to the square of the distance between them.

    Mathematically, this can be written as a proportionality relationship.

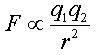
Here q₁ is the relative charge on object 1 which is the core charge or the amount of nuclear force not canceled out by the interference of inner electrons (protons in the nucleus - inner electrons = core charge), q₂ is the relative charge on object 2 (outermost electrons--the reactive electrons) and r² is the distance between the two objects (the distance between the outermost level of electrons and the nucleus).  This is just a proportionality constant and not really an equation that can be used directly.  To use it, a proportionality constant must be found which will allow us to replace the proportionality sign with an equals sign.  However, under constant conditions (ideal for comparing atomic properties), we can just simply ignore the constant since it never changes.  This means we can compare the relative force of attraction between the nucleus and the outermost level of electrons which will verify the periodic trends.  We would have to look up the actual radius for each atom or the formula can be further simplified by replacing radius with period number since each successive period is progressively larger.  This a pretty gross simplification, but for the most part it works satisfactorily.  So in the end, using this formula to verify periodic trends is quite an estimate, but it does serve a rough guide.

    For example, we can use Coulomb's Law to predict that lithium is more reactive than hydrogen. In both cases, there is just one outer electron (thus q₂ is the same = 1) and the core charge is the same (q₁ = 1; no inner electrons in hydrogen; therefore 1 proton - 0 inner electrons = 1 core charge, 3 protons - 2 inner electrons = 1 core charge for lithium).  The distance between the outer electron in lithium is considerably larger than that of hydrogen (radius of hydrogen = 1 and the radius of lithium = 2 based on period numbers). 

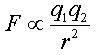
becomes: (1)(1)/1² for hydrogen and (1)(1)/2² or 0.25 for lithium; therefore, F_hydrogen > F_lithium.  Thus the force of the nucleus of lithium exerts less attraction on its outermost electrons compared to hydrogen.  Therefore lithium is more reactive since metals become more reactive as it becomes easier to lose outermost electrons.

    Consider another example comparing lithium and beryllium.  For lithium, q₁= 1, q₂ = 1 and r = 2.  For beryllium, q₁= 2 (4 protons - 2 inner electrons). q₂ = 2 (2 outer electrons) and r = 2 (same period). 

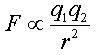
becomes (1)(1)/2² or 0.25 for lithium and (2)(2)/2² or 1 for beryllium; therefore F_beryllim > F_lithium.  This makes sense since we know that metals become less reactive moving left to right within a period due to increasing core charge.  Thus, it is harder to remove the outermost electron in beryllium compared to lithium.

    You can apply the formula to non-metals as well, keeping in mind the non-metals react by gaining electrons so a stronger force of attraction yields higher reactivity. Of course the assumptions used here will not work for the exceptions to periodic trends such as partial stabilization. The formula would work if real values for charges and radii were used, but if you could obtain that data, you could also simply obtain the reactivity data making the use of the formula pointless.

The Quantum Atom

    DeBroglie's recognition of wave-particle duality prompted several prominent physicists to attempt to develop models of the atom employing the wave character of the electron.  The wave/particle duality of nature introduces a complicated limitation to our ability to exactly model the behavior of the electron as was first realized by Werner Heisenberg (1901 - 1976). 

    The duality of matter makes it impossible to develop a set of equations that tells us both exactly where an electron is and what its momentum might be.  This is called the "Heisenberg Uncertainty Principle", a concept that has been badly misused in fields ranging from art to philosophy.  While this seems abstract, what it means is that the wave pictures we are used to thinking about are really pictures of the probability of finding the electron in a given volume of space.  Generally the "orbital" pictures we see indicate the volume of space where we'd expect to have a 90% probability of finding the electron.  In fact, the use of the word "orbital" as opposed to Bohr's "orbit" reflects the fact that we no longer know where the electron "is", but only its probability of being there. 

    In 1925, Heisenberg published a paper in which he developed a model of a quantum mechanical atom utilizing matrix algebra. Although this paper attracted a certain amount of attention (and ultimately won Heisenberg the Nobel Prize in 1932) the mathematics and Heisenberg's presentation was sufficiently obscure that may physicists simply couldn't follow it.  While Heisenberg was developing matrix algebra, Erwin Schrödinger (1887 - 1961) was also seeking the same grail. In contrast to Heisenberg, Schrödinger's development used conventional and readily understood (at least by the physicists and mathematicians of his day) wave equations. Initially, Schrödinger attempted to include relativistic effects in his calculations and finally gave up when he could not get the equations to give reasonable results.  When Schrödinger published his work in January of 1926, it was immediately accepted and appreciated by a wide audience.  The central feature of the paper is the equation now known as the Schrödinger Equation presented below:

    In principle if you can write this equation for anything you can solve for it exactly. In practice, the mathematics is relatively easy for the hydrogen atom and beyond our present ability for anything involving a nucleus and two or more electrons.  It is possible to use various approximation techniques to solve for big atoms and the results are quite good. F or hydrogen, of course, the results are dead on.  A fact that is often overlooked is that the atomic orbitals to be presented below, are actually the orbitals calculated for hydrogen. W e use them for all other atoms even though we recognize that this is a first approximation.  This equation then can be used to define the orbitals that exist within atoms.  These orbitals bear great similarity to the harmonics of the three dimensional wave. 

    Schrödinger's wave equation involved three "constants" called quantum numbers that were used to exactly assign the energy level, orbital, and direction of the electron. Some time after Schrödinger's original publication, Paul Dirac (1902 -1984) developed a full relativistic equation for the atom and found that this more detailed model contained an additional quantum number for the "spin" of the electron. Dirac's equations also had an additional curious feature. They led to both + and - values for the charge on the electron. This was regarded as a quirk of the mathematics until the positron was discovered in 1932 by the American scientist Carl Anderson working at Cal Tech. 

    The four quantum numbers are:

• "n" - primary quantum number, establishes the energy level of an electron in an atom. "n" has values from 1 up to 6  in the periodic table and may be very much higher for excited atoms. 
• "l" - determines whether the electron is in the fundamental or harmonic wave of the particular energy level.  (Sometimes these are referred to as subs-hells) "l"s values are associated with a given kind of orbital. Thus "l" = 0 is an "s" orbital, "l" = 1 is a "p" orbital, "l" = 2 is a "d" orbital, etc. As n increases the number of allowed harmonics increases. For example, for the first energy level, "l" may only have a value of 0, i.e. an "s" orbital. For n = 2, however, "l" can be either 0 or 1, thus there are both "s" and "p" orbitals. For "n" = 3. "l" may have values 0, 1, and 2.
• " m_l" - orientation quantum number, establishes which orbital the electron occupies when there is more than one possibility. For example, there is only one "s" orbital in each level, but there are three "p" orbitals and five "d" orbitals. The "m_l quantum number assigns the electron to a specific orbital. 
• "m_s" - spin quantum number. This relativistic quantum number introduces the strangest of the electron's properties: spin.  The equations that describe this property are identical to equations that would describe a spinning top.  In this case, the spinning electron is charged so its spin creates a little magnetic field.  This important quantity makes it possible for two electrons to occupy each atomic orbital, so long as the two electrons have opposite spins. We usually treat spins as "up" or "down" even though these directions have no real physical meaning.  This means that no two atoms will have exactly the same quantum numbers which is referred to as Paulie's Exclusion Principle.

    The following visual image illustrates the energy levels of the atom as described by the combined Schrödinger/Dirac equations. 

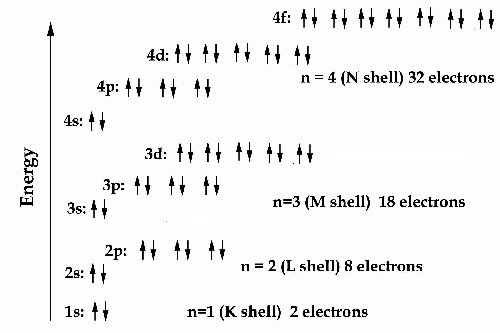
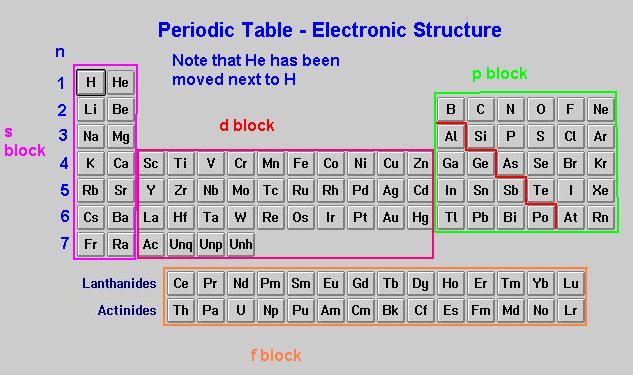
    Each orbital in this energy picture may hold two electrons.  If you look at the periodic table in terms of quantum mechanics, a clear pattern develops as quantum blocks are recognized. 

    Using the Aufbau Principle of filling lower energy levels first, we see that the first two electrons go into the 1s orbital (obviously, one must be spin "up" and the other spin "down".)  Since the 1s level is filled, the third electron must to into the 2s level. This means that Li (with 3 electrons) has its outermost electron in the 2s.  The fourth electron fills the 2s, so the fifth electron must go into the 2p. We'll come back to some details of this filling in a bit. electrons 5 - 10 must go into the 2p level, and, since the 2 level is now full, electron 11 must go into the 3s. Again, electron 12 fills the 3s and electrons 13 -18 go into the 3p.  Although our simple model would suggest that electron 19 should go into the 3d, the position of potassium (K) tells us that something odd is going on. The outermost electrons of K and Ca are "s" electrons and these must be the 4s level.  Since the periodic table must be right, we don't begin filling the 3d orbitals until we get to element 21, scandium.  The simplest way to envision the problem is that the energy gap between the "n" levels decreases as "n" increases.  Thus the n = 3 level is closer in energy to n = 2 than n = 2 is to n = 1.  The 4s level actually has a slight overlap with the 3d resulting in the 4s orbitals filling before the 3d, in agreement with the periodic table. 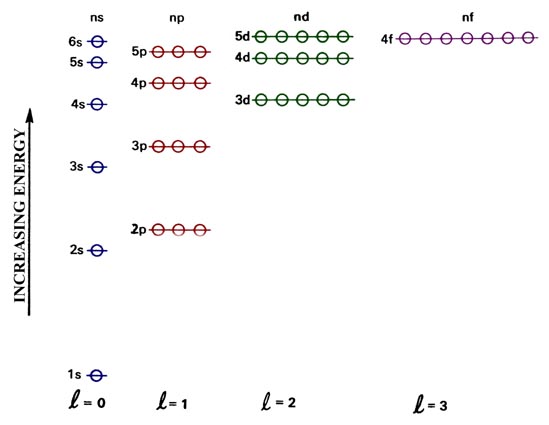Thus the orbital filling diagram needs to be modified to reflect this.  The following schematic is typically used to order orbitals from lowest to highest energy level.

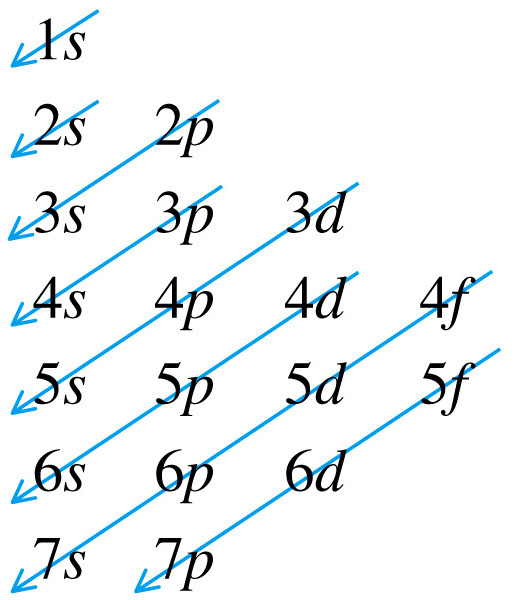
    Therefore, the diagram above should really look like the following to reflect the fact that 4s is lower in energy than 3d.:

    Remembering that electrons do repel one another, it is reasonable to conclude that having two of them in the same orbital would be a higher energy condition than having them in different orbitals. We can establish a simple rule that electrons will tend to singly occupy orbitals until forced to begin pairing up.  This is referred to as Hund's rule.  It turns out that the spin parallel condition is actually the lower
energy case. Unpaired electrons in sub-levels with degenerate orbitals (p, d, f, etc.) will tend to have their spins parallel.  Related to this slight extra stability of parallel spins is the observation by Fredrick Hund, half filled and filled sub-levels have unusual stability. Thus three electrons in the p level or five in the d tend to be far more stable than might be expected.  Additionally, a filled p or d level is even more
stable and it is difficult to remove electrons from these levels once they are filled. The obvious example of this is the inert gases (Group 18) whose stability comes from their filled s and p orbitals. 

    Although the energy level diagrams we have been using are an excellent way to represent the electronic configurations of atoms, we often don't need quite as much detail.  It is appropriate to introduce a shorthand electronic configuration at this point. In this notation, we specify only the "n" and "l" quantum numbers and indicate by a superscript the number of electrons in the various levels.  For example, the electronic configurations of the elements H - Ne are given below: 

     H = 1s¹
     He = 1s²
     Li = 1s²2s¹
     Be = 1s²2s²
     B = 1s²2s²2p¹
     C = 1s²2s²2p²
     N = 1s²2s²2p³
     O = 1s²2s²2p⁴
     F = 1s²2s²2p⁵
     Ne = 1s²2s²2p⁶

    While this is a useful shorthand it does sacrifice information. For example, this notation does not suggest the fact that the p level of nitrogen is half filled.   We would expect chromium to have an electronic configuration of : 

Cr = 1s² 2s²2p⁶3s²3p⁶4s²3d⁴ 

    Experiments show, however, that the real configuration for chromium atoms is: 

Cr = 1s² 2s²2p⁶3s²3p⁶4s¹3d⁵

    If you recall, the 4s level is only slightly lower in energy than the 3d.  Close enough that the additional stabilization gained by half filling the 3d level more than makes up for the energy necessary to promote the electron out of the 4s. The same thing is observed for copper which might be expected to have the electronic configuration: 

Cu = 1s² 2s²2p⁶3s²3p⁶4s²3d⁹ 

but is actually found to have the configuration: 

Cu = 1s² 2s²2p⁶3s²3p⁶4s¹3d¹⁰

in which the d level is filled.  In both the Cr and Cu cases we see Hund's rule in practice. 

    As we go down the Periodic Table we encounter additional cases where the predicted and actual electronic configurations are different.  In addition to Mo, W, Ag and Au that we might expect, Ta has the electronic configuration: 

Ta = 1s² 2s²2p⁶3s²3p⁶4s²3d¹⁰4p⁶ 5s¹4d⁴

in which the 5s electron moves to the 4d even though the d level isn't quite half-filled. 

Perhaps even more surprising is Pd which has the electronic configuration: 

Pd = 1s² 2s²2p⁶3s²3p⁶4s²3d¹⁰4p⁶ 5s⁰4d¹⁰

in which both of the 5s electrons have been promoted to fill the 4d.   You would not really write 5⁰ since it is empty.  Finally, we should note that writing out these electronic configurations does get tedious. Short hand electronic configurations can be written by substituting the appropriate noble gas for the core electrons followed by the outermost or valence electrons.  Here you may write the configurations of Cr and Pd as: 

     Cr = [Ar]4s¹3d⁵
     Pd = [Kr]4d¹⁰

because 

Ar = 1s² 2s²2p⁶3s²3p⁶
Kr = 1s² 2s²2p⁶3s²3p⁶4s²3d¹⁰4p⁶

Lewis Diagrams

    Generally the electrons that will be involved in bonding (of whatever kind) will be the valence electrons. These are the electrons on    the outer perimeter of an atom.  The number of valence electrons for an atom is often, but not always, determined from the position of that element on the periodic table.  A handy way to illustrate these valence electrons is to use Lewis diagrams, also called electron dot diagrams.  These diagrams show the symbol of the element with as many dots around it as there are electrons in the outermost energy level. For example, sulfur with its electron configuration of 1s²2s²2p⁶3s²3p⁴ has six valence electrons and the Lewis diagram is the symbol S with six dots around it, representing those three valence electrons. 

    Notice that there is a pattern to the placement of the electrons around the symbol.  The symbol itself represents the core electrons and the valence electrons are placed in a way to represent the s and p orbitals obeying Hund's rule.  Thus p orbitals are filled one at a time until all have one electron, then electron pairing can take place.  It should be noted that since electrons and atoms themselves are spinning and moving about, this diagram is a convention only and can be modified as needed to reflect proper geometry such as in bonding.

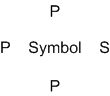
    Lewis diagrams are useful and easy to draw for the representative elements, which are the Group I-A and II-A metals and the nonmetals.  However, because of the overlapping energy sub-levels, these electron dot diagrams become more challenging for the transition metals, so we won't bother with Lewis diagrams for them.