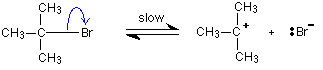
Carbon-bromine bonds are reasonably strong, so this
is a slow change. If the ions hit each other again, the covalent bond will
reform. The curly arrow in the equation shows the movement of a pair of
electrons. If there is a high concentration of hydroxide ions present,
the positive ion stands a high chance of hitting one of those. This step
of the overall reaction will be very fast. A new covalent bond is made
between the carbon and the oxygen, using one of the lone pairs on the oxygen
atom.
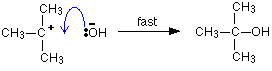
Because carbon-oxygen bonds are strong, once the OH
group has attached to the carbon atom, it tends to stay attached.
The mechanism shows that the reaction takes place in two steps and describes
exactly how those steps happen in terms of bonds being broken or made.
It also shows that the steps have different rates of reaction - one slow
and one fast.
The overall rate of a reaction (the one which you
would measure if you did some experiments) is controlled by the rate of
the slowest step. In the example above, the hydroxide ion can't combine
with the positive ion until that positive ion has been formed. The second
step is in a sense waiting around for the first slow step to happen. The
slow step of a reaction is known as the rate determining step. As long
as there is a lot of difference between the rates of the various steps,
when you measure the rate of a reaction, you are actually measuring the
rate of the rate determining step.
Here is the mechanism we have already looked at.
How do we know that it works like this?
By doing rate of reaction experiments, you find this
rate equation:
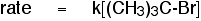
The reaction is first order with respect to the organic
compound, and zero order with respect to the hydroxide ions. The concentration
of the hydroxide ions isn't affecting the overall rate of the reaction.
If the hydroxide ions were taking part in the slow step of the reaction,
increasing their concentration would speed the reaction up. Since their
concentration doesn't seem to matter, they must be taking part in a later
fast step. Increasing the concentration of the hydroxide ions will
speed up the fast step, but that won't have a noticeable effect on the
overall rate of the reaction. That is governed by the speed of the slow
step. In a simple case like this, where the slow step of the reaction
is the first step, the rate equation tells you what is taking part in that
slow step. In this case, the reaction is first order with respect to the
organic molecule - and that's all. This gives you a starting point
for working out a possible mechanism. Having come up with a mechanism,
you would need to find more evidence to confirm it. For example, in this
case you might try to detect the presence of the positive ion that is formed
in the first step.
Changing the concentration of substances taking part
in a reaction usually changes the rate of the reaction. A rate equation
shows this effect mathematically. Orders of reaction are a part of the
rate equation. There are several simple ways of measuring a reaction rate.
For example, if a gas was being given off during a reaction, you could
take some measurements and work out the volume being given off per second
at any particular time during the reaction. A rate of 2 cm3
s-1 is obviously twice as fast as one of 1 cm3 s-1.
However, for this more formal and mathematical look at rates of reaction,
the rate is usually measured by looking at how fast the concentration of
one of the reactants is falling at any one time. For example, suppose you
had a reaction between two substances A and B. Assume that at least one
of them is in a form where it is sensible to measure its concentration
- for example, in solution or as a gas. For this reaction you could
measure the rate of the reaction by finding out how fast the concentration
of, say, A was falling per second. You might, for example, find that
at the beginning of the reaction, its concentration was falling at a rate
of 0.0040 mol dm3 s-1. This means that every
second the concentration of A was falling by 0.0040 moles per cubic decimeter.
This rate will decrease during the reaction as A gets used up.
Orders of reaction are always found by doing experiments.
You can't deduce anything about the order of a reaction just by looking
at the equation for the reaction. So let's suppose that you have
done some experiments to find out what happens to the rate of a reaction
as the concentration of one of the reactants, A, changes. Some of the simple
things that you might find are:
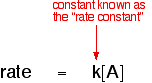
1. One possibility: The rate of reaction is proportional to the concentration
of A which means that if you double the concentration of A, the rate doubles
as well. If you increase the concentration of A by a factor of 4, the rate
goes up 4 times as well. You can express this using symbols as:
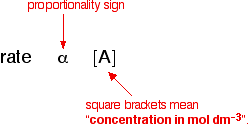
Writing a formula in square brackets is a standard
way of showing a concentration measured in moles per cubic decimeter (liter).
You can also write this by getting rid of the proportionality sign and
introducing a constant, k.
2. Another possibility: The rate of reaction is proportional to the
square of the concentration of A which means that if you doubled the concentration
of A, the rate would go up 4 times (22). If you tripled the concentration
of A, the rate would increase 9 times (32). In symbol terms:
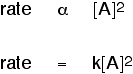
Thus by doing experiments involving a reaction between
A and B, you would find that the rate of the reaction was related to the
concentrations of A and B in this way:
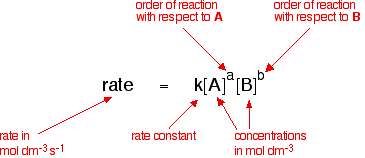
This is called the rate equation for the reaction.
The concentrations of A and B have to be raised to some power to show how
they affect the rate of the reaction. These powers are called the orders
of reaction with respect to A and B.
If the order of reaction with respect to A is 0 (zero),
this means that the concentration of A doesn't affect the rate of reaction.
Mathematically, any number raised to the power of zero (x0)
is equal to 1. That means that that particular term disappears from the
rate equation.
If the order of reaction with respect to A is >1,
this means the concentration of A is causing the reaction to speed up by
some factor. However, if the order of reaction with respect to A
is <0 or negative, this means that the concentration of A is causing
the reaction to slow down by some factor. Note that a negative exponent
could have just been written as a decimal or fraction in which case the
order of reaction would be between 0 and 1 but not including 0 or 1.
The exponents are not usually written in this manner though.
The overall order of the reaction is found by adding
up the individual orders. For example, if the reaction is first order with
respect to both A and B (a = 1 and b = 1), the overall order is 2. We call
this an overall second order reaction.
It doesn't matter how many reactants there are. The
concentration of each reactant will occur in the rate equation, raised
to some power. Those powers are the individual orders of reaction. The
overall order of the reaction is found by adding them all up.
A fundamental challenge in chemical kinetics is the
determination of the reaction order (or, in general, the Rate Law) from
experimental information. We know that the rate law closely related to
the reaction mechanism, and the knowledge of the mechanism of a given reaction
allows us to control that reaction. But how does one actually determine
a rate law? The first step is to control the conditions under which a reaction
occurs, and then determine the rate of that reaction. If we measure the
reaction rate just after we define the reaction conditions, then this is
a measurement of the initial rate of the reaction.
Consider a reaction A + B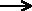 
Products. An experimenter prepares a reaction mixture of 1.00 M of each
of the reactants and measures the rate of reaction initially (at very early
times, i.e. before the reactant concentrations have had a chance to change
much due to the progress of the reaction) to be 1.25 x 10-2
M/s. What is the rate constant for the reaction? You cannot determine
this from the above information, because first you have to know the reaction
order! The reaction stoichiometry does NOT determine the reaction
order except in the special case of an ELEMENTARY reaction. (An elementary
reaction is one in which the reaction takes place with a mechanism implied
by the reaction equation. Most reactions are NOT elementary)
More information about the reaction rate law is needed
than a single measurement of an initial rate! In order to determine the
rate law experimentally, we must use more than one measurement of rate
versus concentration!
So in our reaction of A + B
Products the experimenter prepares several reaction mixtures and determines
the initial reaction rates under these different conditions. The data obtained
for several experimental runs in tabulated below
|
Run # |
Initial [A]
([A]0) |
Initial [B]
([B]0) |
Initial Rate
(v0) |
|
1 |
1.00 M |
1.00 M |
1.25 x 10-2 M/s |
|
2 |
1.00 M |
2.00 M |
2.5 x 10-2 M/s |
|
3 |
2.00 M |
2.00 M |
2.5 x 10-2 M/s |
Before we do anything, we must determine the order
of the reaction with respect to every reactant, i.e. we must determine
the rate law for the reaction. In the above example, the order can be easily
determined by inspection. Find a pair of experimental runs that the concentration
of only one reactant changes. This is called the method of isolation and
a good experimental design always has one such pair of experimental runs.
We can see that in runs 1 and 2, only the initial concentration of B has
been varied. In fact, [B]0 has doubled from run 1 to run 2 and the reaction
rate has also doubled. Therefore the reaction must be First Order in B.
Examination of runs 2 and 3 show that in these experimental runs the concentration
dependence of A has been isolated. In this case the doubling of the initial
concentration of A has no effect on the reaction rate so the reaction must
be Zeroth Order in A.
Thus the rate law for the reaction is
rate = k[B]1[A]0 = k[B]
Now, the rate constant can be determined from any
of the experimental runs. Let's substitute the values of trial # 3 into
our rate law.
rate = 2.5 x 10-2 M/s= k (2.0 M) and thus k =
1.25 x 10-2 s-1
But some rate laws are more complex. Consider
a reaction A + B + C
Products Several initial conditions of this reaction are investigated
and the following data are obtained:
|
Run # |
[A]0 |
[B]0 |
[C]0 |
v0 |
|
1 |
0.151 M |
0.213 M |
0.398 M |
0.480 M/s |
|
2 |
0.251 M |
0.105 M |
0.325 M |
0.356 M/s |
|
3 |
0.151 M |
0.213 M |
0.525 M |
1.102 M/s |
|
4 |
0.151 M |
0.250 M |
0.480 M |
0.988 M/s |
Isolate the effect of the concentration of one of
the reactants. In runs number 1 and 3, the only change of initial concentrations
is that of reactant C, a change from 0.398 M to 0.525 M with a change in
rate from 0.480 M/s to 1.102 M/s. These numbers are not so easy as to be
able to guess the order by inspection, so lets think mathematically. If
we define the order of the reaction in reactants A, B, and C as a, b, and
c, we can write down the rate law (with unknown orders): rate = k [A]a [B]b [C]c
The ratio of the initial rates of runs 1 and 3 is
then:
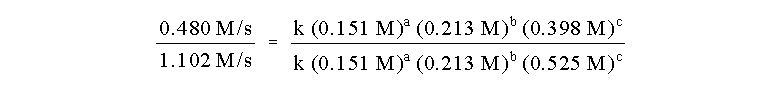
Note that we have chosen this ratio so that many
terms on the right hand side cancel, i.e. k and the concentrations of species
A and B. The ratio reduces to:
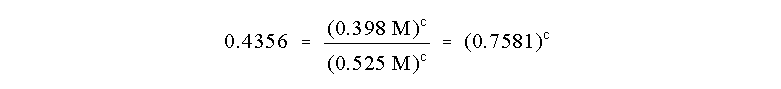
Note that none of the numbers in this equation have
any units anymore because we have divided them out in a dimensionless ratio.
Now, how to solve for c? Take the natural log or ln of both sides of the
equation
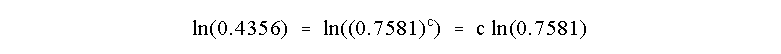
which allows us to determine that
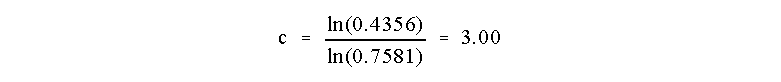
So the reaction is Third Order in reagent C!
To continue, we pick another pair of runs that have a change in the initial
concentration of just one reactant and repeat the math we just did; however,
there are no such cases in this experiment. So instead we pick another
pair of runs that changes in just one variable besides C. We already know
the exponent for C so it is no longer an unknown. This simplifies
our work. Let us choose the runs 1 and 4. The ratio of the initial
rates of these runs is:
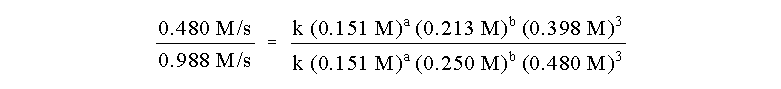
Note that everything cancels, is known, or is the
order b. So:
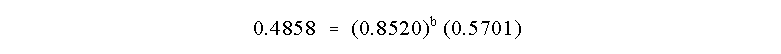
We can determine b as before by taking the ln of
both sides of this equation:
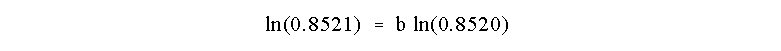
and b = 1.00. The reaction is First Order in B!
Now that we know the order of Reactants A and B, we can
use another pair of experimental runs to determine the remaining unknown
order. We must use a pair of runs where the initial concentration of A
changes, so we pick runs 1 and 2. As before, the ratio of initial rates
is
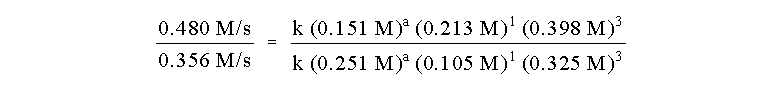
The rate constant cancels as before and we can solve for a:
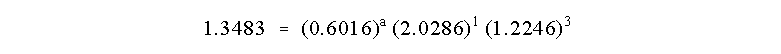
and, as usual, take the ln of both sides:
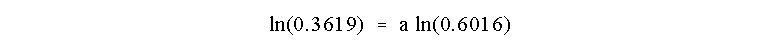
which results in a = 2.00 and the reaction is Second Order in A.
The rate constant for the reaction may now be evaluated from any of
the experimental runs:
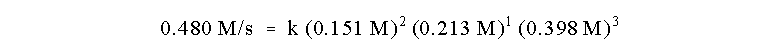
or k = 1.57 x 103 L5 mol-5s-1
These units are appropriate for a reaction that is
sixth order overall. Use another experimental run to check your answer.
If the rate law is correct, every experimental run will give the same value
of the rate constant.
A first-order reaction is one where the rate depends
on the concentration of the species to the first power. For a general unimolecular
reaction, A products
the reaction rate expression for a first order reaction is rate = k[A]0
= k[A]. We also can write that rate = change in [A]/change in time
or R = -d[A]/dt (negative because we are slowing down). Thus we get
R = -d[A]/dt = k[A]
Rearranging this we get:
d[A]/[A] = -kdt
This equation defines any
population change in nature and so we recognize it as a factor of the natural
exponent e. That is, things changing according to this equation are
governed by the rate of change corresponding to the natural log or e which
is a log to the base of 2.718. You may be used to log which is to
the base of 10. Thus the log of 10 = 1 and the log of 100 = 2.
Note that this log really is written as log10 but the 10 is
assumed. We could also look at log2 of 8 = 3 or the log7
of 49 = 2. In the case of first order reactions we are looking at
the loge which s really ln. Thus the reverse ln = e just
as the antilog7 of 2 = 49.
This gives us an equation for the first order decay:
[A]/[A]0 = e-kt
where [A]0 is the initial concentration, [A] is the concentration
after some time = t and k is the rate law constant. If t = the time
for 50% of [A]0 to decompose, the equation becomes 0.5 = e-kt.
This time span is referred to as the half life for that substance.
Taking the ln of both sides reduces this equation to 0.693 = kt.
Thus if we know the time for one half life, we can always determine the
value of k which can then be used to predict any concentration change over
time.
Consider this example. If the half life
of a sample is 12.5 hours, what percentage of a 0.25 g sample remains after
13.7 hours.
0.693 = kt
0.693 = k(12.5)
k = 0.693/12.5 = 0.05544 hours-1
substituting into [A]/[A]0 = e-kt
[A]/0.25 = e-(0.05544)(13.7)
[A]/0.25 = e-0.759528
[A]/0.25 = 0.4679
[A] = (0.4679)(0.25) = 0.117 g.
Temperature of the Reaction
As you increase the temperature the rate of reaction
increases. As a rough approximation, for many reactions happening
at around room temperature, the rate of reaction doubles for every 10°C
rise in temperature. You have to be careful not to take this too literally.
It doesn't apply to all reactions. Even where it is approximately true,
it may be that the rate doubles every 9°C or 11°C or whatever.
The number of degrees needed to double the rate will also change gradually
as the temperature increases. Some reactions are virtually instantaneous
- for example, a precipitation reaction involving the coming together of
ions in solution to make an insoluble solid, or the reaction between hydrogen
ions from an acid and hydroxide ions from an alkali in solution.
So heating one of these won't make any noticeable difference to the rate
of the reaction. Almost any other reaction you care to name will
happen faster if you heat it - either in the lab, or in industry.
Particles can only react when they collide. If you
heat a substance, the particles move faster and so collide more frequently.
That will speed up the rate of reaction. That seems a fairly straightforward
explanation until you look at the numbers! It turns out that the
frequency of two-particle collisions in gases is proportional to the square
root of the kelvin temperature. If you increase the temperature from 293
K to 303 K (20°C to 30°C), you will increase the collision frequency
by a factor of 1.7% for a 10° rise. The rate of reaction will probably
have doubled for that increase in temperature - in other words, an increase
of about 100%. The effect of increasing collision frequency on the rate
of the reaction is very minor.
The important effect is quite different, that being
activation energy. Collisions only result in a reaction if the particles
collide with enough energy to get the reaction started. This minimum energy
required is called the activation energy for the reaction. You can
mark the position of activation energy on a Maxwell-Boltzmann distribution
to get a diagram like this:
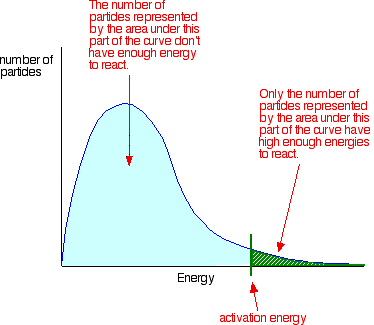
Only those particles represented by the area to the
right of the activation energy will react when they collide. The great
majority don't have enough energy, and will simply bounce apart.
To speed up the reaction, you need to increase the number of the very energetic
particles - those with energies equal to or greater than the activation
energy. Increasing the temperature has exactly that effect - it changes
the shape of the graph. In the next diagram, the graph labeled T
is at the original temperature. The graph labeled T+t is at a higher temperature.
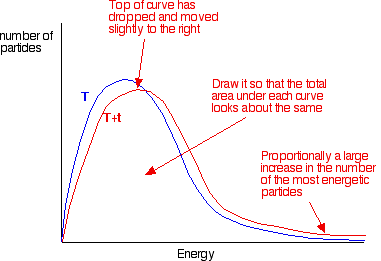
If you now mark the position of the activation energy,
you can see that although the curve hasn't moved very much overall, there
has been such a large increase in the number of the very energetic particles
that many more now collide with enough energy to react.
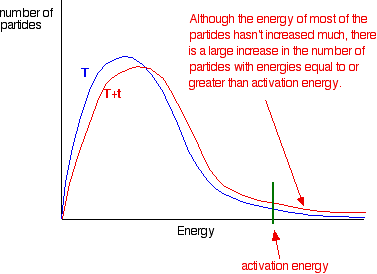
Remember that the area under a curve gives a count
of the number of particles. On the last diagram, the area under the higher
temperature curve to the right of the activation energy looks to have at
least doubled - therefore at least doubling the rate of the reaction.
Increasing the temperature increases reaction rates because of the disproportionately
large increase in the number of high energy collisions. It is only these
collisions (possessing at least the activation energy for the reaction)
which result in a reaction.
Addition of a Catalyst
A catalyst is a substance which speeds up a reaction,
but is chemically unchanged at the end of the reaction. When the reaction
has finished, you would have exactly the same mass of catalyst as you had
at the beginning. Consider some examples:
- Decomposition of hydrogen peroxide by manganese(IV) oxide, MnO2
- Nitration of benzene by concentrated sulphuric acid
- Manufacture of ammonia via the Haber Process by iron
-
Conversion of SO2 into SO3 during the Contact Process
to make sulphuric acid by vanadium(V) oxide, V2O5
- Hydrogenation of a C=C double bond by nickel
Again the critical factor is activation energy.
Collisions only result in a reaction if the particles collide with enough
energy to get the reaction started. This minimum energy required is called
the activation energy for the reaction. You can mark the position of activation
energy on a Maxwell-Boltzmann distribution to get a diagram like this:
Only those particles represented by the area to the
right of the activation energy will react when they collide. The great
majority don't have enough energy, and will simply bounce apart.
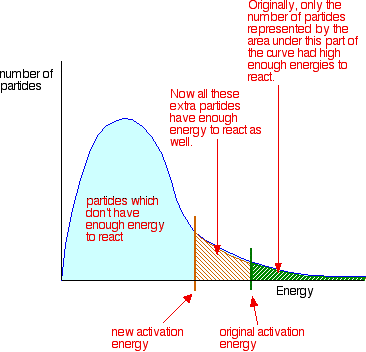
To increase the rate of a reaction you need to increase the number of successful
collisions. One possible way of doing this is to provide an alternative
way for the reaction to happen which has a lower activation energy.
In other words, to move the activation energy on the graph like this:
Adding a catalyst has exactly this effect on activation
energy. A catalyst provides an alternative route for the reaction. That
alternative route has a lower activation energy. Showing this on an energy
profile:
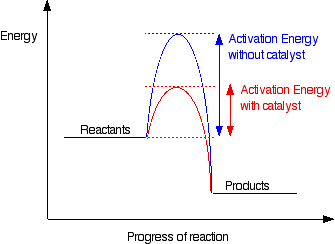
Thus a catalyst provides an alternative route for
the reaction with a lower activation energy. It does not actually
lower the activation energy of the reaction. There is a subtle difference
between the two statements that is easily illustrated with a simple analogy.
Suppose you have a mountain between two valleys so that the only way for
people to get from one valley to the other is over the mountain. Only the
most active people will manage to get from one valley to the other.
Now suppose a tunnel is cut through the mountain. Many more people will
now manage to get from one valley to the other by this easier route. You
could say that the tunnel route has a lower activation energy than going
over the mountain. But you haven't lowered the mountain! The tunnel has
provided an alternative route but hasn't lowered the original one. The
original mountain is still there, and some people will still choose to
climb it. In the chemistry case, if particles collide with enough energy
they can still react in exactly the same way as if the catalyst wasn't
there. It is simply that the majority of particles will react via the easier
catalyzed route.
X)
that occurs during a given period of time (
.
