Enthalpy
Thermochemistry deals with transfers of energy between
reacting chemicals and the world around them. The word system refers to
that particular part of the universe we wish to study. The system
might be the chemicals reacting in a beaker or the chemicals in a battery
cell reacting to give electricity, or the system of a living cell.
The word surroundings refers to whatever is entirely outside the defined
system, everything in the universe except the system itself. A boundary,
real or imaginary, separates the system from its surroundings. When the
system is in a beaker, the boundary exists wherever the solution contacts
the beaker or the air above it. If the boundary can prevent any transfer
of heat between the system and the surroundings, we say that the system
is insulated from its surroundings. Styrofoam makes a good insulating boundary
for keeping a cup of coffee hot, but no material is a perfect insulator.
Another term that is used frequently is the state
of a system. Each system has a state defined by listing its temperature,
pressure, volume, and composition (including concentration terms).
We say that a system undergoes a change of state whenever any change occurs
in one or more of the variables that define the system.
In thermochemistry we are concerned with the exchange
of energy between a chemical system and its surroundings. Sometimes chemical
changes are able to bring energy into the system. These are endothermic
changes. An example is the charging of a battery, in which energy from
an external source becomes stored in the battery in the form of chemical
potential energy. Photosynthesis is also endothermic as far as the plant
is concerned, and the needed energy (only 0.04%) is imported from the sun.
When endothermic changes occur by themselves within an uninsulated system,
we often notice a cooling effect in the surroundings. This is what happens
to cool your drink with ice or when you use an "instant cold" compress
from the drugstore.
Many chemical reaction are able to release energy
to the surroundings. Such changes are described as exothermic. A typical
example is the combustion of gasoline. Heat transfer away from the system
(if uninsulated) and into the surroundings, where the temperature increases.
The form of the energy absorbed or released during
a change can vary. It sometimes appears as light, or electrical work,
but most often occurs only as heat. When the entire energy change
of a reaction involves heat, the amount of heat is called the heat of reaction
and is usually represented by the symbol 'Q'.
We show exothermic reactions by -Q meaning that energy
has been lost from the system. Endothermic reactions are documented by
+Q meaning that energy was absorbed by the system. The actual amount
of heat of reaction for a given change in a system depends to some extent
on the conditions under which we carry out the reaction. It depends on
the physical states of the reactants and products; it depends on the initial
temperature of the system; and it depends somewhat on whether the volume
of the system or its pressure is held constant or is permitted to change.
To simplify matters a great deal, chemists noticed a long time ago that
most reactions are carried out in open beakers or vats under atmospheric
pressure. So we will also limit ourselves to these conditions and
some new terms to explain these conditions.
Enthalpy, refers to the total value of energy of
a system when it is at constant pressure. It is symbolized by the letter
'H'. When a system reacts at constant pressure it will either gain or lose
energy and we say that the enthalpy of the system has gone through a change
or an enthalpy change, which is symbolized by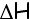 
means "change in". As a result we look at:
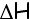= Hfinal - Hinital
where Hfinal is the enthalpy of the system in its final state
and Hinitial is the enthalpy of the system in its initial state.
For a chemical reaction the above equation can be expressed much more nicely
as:
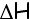= Hproducts - Hreactants
The above equation simply put means "the total heat
content of the products minus the total heat content of all the reactants".
After having gone to all this effort to give a formal definition of H,
it is perhaps a bit disappointing to learn that we cannot actually calculate
it from measured values of Hfinal and Hinitial. This
is because the total enthalpy of the system depends on its total kinetic
energy plus its total potential energy, and these values can never be determined.
The good news is that we don't need to know it. We care only about what
our system could do for us (or to us!) right here at a particular place
on this planet. For example, when we want to know the yield of energy from
burning gasoline, we really do not care what its total enthalpy is in either
its initial or final state. All we care about is by how much the enthalpy
changes, because it is only this enthalpy change that is available to us.
In other words, we don't need Hinital and Hfinal
, but we can calculate H (released or added) by direct measurement.
Enthalpy is a particularly important state function.
The enthalpy of a system in a given state cannot depend on how the system
arrived in that state. This is useful to know, because when we measure
the heat of a reaction we do not have to worry about how the reaction is
occurring, but only that it is. To determine H, we only have to be sure
of our initial and final states and then measure the total amount of heat
absorbed or evolved as the system changes between these states.
Consider the following series of energy changes (don't
worry about what the entire reaction is doing):
-
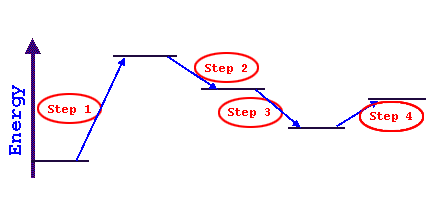
step 1 is endothermic since the products are less stable and possess more
energy than the reactants (energy was added and thus temperature drops)
-
steps 2 and 3 are both exothermic since in each case the products possess
less energy (more stable) than the respective reactants (energy was released
and thus temperature increases)
-
step 4 is endothermic since the products possess more energy than the reactants
(energy was added and thus temperature drops)
Hess's Law
Chemical scientists have agreed upon a standard conditions
for temperature and pressure. These conditions have of course been
chosen so that experiments can be done easily. Thus the standard reference
temperature is 25oC, which is just slightly above normal room
temperature. This is easily controlled in a water bath. The reference pressure
is 1 atmosphere or 101.325 kPa. Together they are referred to STAP.
When the enthalpy change of a reaction is determined
with all reactants and products at 1 atm and some given temperature, and
when the scale of the reaction is in the moles specified by the coefficients
of the equation, then H is the standard enthalpy change or the standard
heat of reaction. To show that a pressure of 1 atm is used, the symbol
H is given a superscript, o, to make the symbol Ho. Values of
Ho usually correspond to an initial and final temperature of
25oC, unless otherwise specified. The units of Ho
are normally kilojoules. For example, a reaction between gaseous nitrogen
and hydrogen produces gaseous ammonia according to the equation
N2(g) + H2(g)
2 NH3(g)
When 1.00 mol of N2 react with 3.00 mol
of H2 to form 2.00 mol of NH3 at STAP, the reaction
releases 92.38 kJ. Hence for the reaction as written Ho = -92.38 kJ.
Often it is useful to make the enthalpy change of
a reaction part if its equation. When we do this we have to be very careful
about the coefficients, and we must indicate the physical states of all
the reactants and products. The reaction between gaseous nitrogen and hydrogen
to form gaseous ammonia, for example, releases 92.38 kJ is 2.00 mol of
NH3 forms.
But if we were to make twice as much, or 4.00 mol,
of NH3 from 2.00 mol of N2 and 6.00 mol of H2,
then twice as much heat (184.8 kJ) would be released. On the other hand,
if only 0.50 mol of N2 and 1.50 mol of H2 were to
react to form only 1.00 mol of NH3, then only half as much heat
(46.19 kJ) would be released.
An equation that includes its value of Ho
is called a thermochemical equation. The following three thermochemical
equations for the formation of ammonia, for example, give the quantitative
data describe in the preceding paragraph and correctly specify the physical
states of all substances.
| N2(g) + 3 H2(g)
2 NH3(g) |
Ho = -92.38 kJ |
| 2 N2(g) + 6 H2(g)
4 NH3(g) |
Ho = -184.8 kJ |
| ½ N2(g) + 1½ H2(g)
NH3(g) |
Ho = -46.19 kJ |
When you read a thermochemical equation, always interpret
the coefficient as moles. This is why we must use fractional coefficients
in such an equation, where normally we try to avoid them (because we cannot
have fractions of molecules). In thermochemical equations, however, fractions
are allowed, because we can have fractions of moles.
Once we have the thermochemical equation for a particular
reaction, we automatically have all the information we need for the reverse
reaction. The thermochemical equation for the combustion of carbon to give
carbon dioxide is:
C(s) + O2(g)
CO2(g) Ho = -393.5 kJ
The reverse reaction would be experimentally impossible
to perform, for reasons that will become clear later. But from the above
equation we can write the reverse reaction.
CO2 (g) C(s)
+ O2(g) Ho = +393.5 kJ
If we have the Ho for a given reaction,
the Ho for the reverse reaction has the same numerical value,
but its algebraic sign is reversed.
When thermochemical equations are added to give some
new equation, their values of Ho are also added to give the Ho of the new
equation. The enthalpy change for a reaction is a state function. Its value
is determined only by the enthalpies of the initial and final states of
the chemical system, and not by the path taken by the reactant as they
form the products. To appreciate the significance of this, let us consider
again the combustion of carbon.
C(s) + O2(g)
CO2(g) Ho = -393.5 kJ
This is only one possible way to make CO2.
The second pathway to CO2 involves two steps. The first is the
combination of carbon with just enough oxygen to form carbon monoxide.
Then, in the second step, this CO is burned in additional oxygen to produce
CO2. Both steps are exothermic, and their thermochemical equations
are:
| C(s) + ½O2(g)
CO(g) |
Ho = -110.5 kJ |
| CO(g) + ½O2(g)
CO2(g) |
Ho = -283.0 kJ |
Note that if we add the amount of heat liberated
in the first step to the amount released in the second, the total is the
same as the heat given off by the one-step reaction that was described
first. (-110.5 kJ) + (-283.0) = -393.5 kJ The total decrease
in energy, however, is the same regardless of which path is taken, so the
total energy evolved in the two-step path has to be the same as in the
one-step reaction.
This is the Law of Heat Summation (Hess's Law) which states that
for any reaction that can be written in steps, the standard heat of reaction
is the same as the sum of the standard heats of reactions for the steps.
One of the most useful applications of Hess's law
is the calculation of the value of Ho for a reaction whose Ho
is unknown or cannot be measured. Hess's law says that we can add thermochemical
equations, including their values of Ho, to obtain some desired
thermochemical equation and its Ho.
Consider the following example: Carbon monoxide
is often used in metallurgy to remove oxygen from metal oxides and thereby
give the free metal. The thermochemical equation for the reaction of CO
with iron(III) oxide, Fe2O3, is
Fe2O3(s)
+ 3 CO(g) 2
Fe(s) + 3 CO2(g)
Ho = -26.74 kJ
Use this equation and the equation for the combustion of CO
CO(g) + ½O2(g)
CO2(g) Ho = -283.0
kJ
to calculate the value of Ho for the reaction
2 Fe(s)
+ 1½O2(g)
Fe2O3
Combine the equations in such a way that we
can add them to the final target equation. Then we add the corresponding
Ho's to obtain the Ho of the target equation. The
target equation must have 2 Fe on the left, but the first equation above
has 2 Fe on the right. To move it left, reverse the entire equation
and remember to reverse the sign of Ho. When the equation is
flipped over the Fe2O3 also falls into the correct
position.
2 Fe(s)
+ 3 CO2(g) Fe2O3(s)
+ 3 CO(g)
Ho = +26.74 kJ
There must be 1½O2 of the left,
and we must be able to cancel three CO and three CO2 when the
equations are added. Multiply the second equation by 3 and we get
the necessary coefficients. Multiply the Ho values for the second
equation by 3 as well.
3 CO(g)
+ 1½O2(g)
3 CO2(g)
Ho = 3(-283.0 kJ) = -849.0 kJ
If we then sum our equations we get the equation
we want. If we sum the Ho we get the value we were looking
for.
2 Fe(s)
+ 3 CO2(g) Fe2O3(s)
+ 3 CO(g)
Ho = +26.74 kJ
3 CO(g)
+ 1½O2(g)
3 CO2(g)
Ho = -849.0 kJ
____________________________________________________________
2 Fe(s)
+ 1½O2(g)
Fe2O3
Ho = +26.74 kJ + -849.0 kJ = -822.26 kJ
Notice that some species cancel out of the reactions
when you sum them.
If you look at the reactions when you are summing
them, it becomes apparent the the summation of the heat terms always follow
a predictable pattern which is 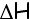o
= [Hoproducts] - [Horeactants]
What goes into the products and reactants brackets
are the standard heats of formation. We'll begin by the defining the term
standard state. Any substance in its most stable physical form (gas, liquid,
or solid) at 25oC and under a pressure of 1 atm is said to be
in its standard state. The element oxygen for example, is in its standard
state when its exists as a molecule of O2 -not as atoms and
not as molecules of O3. The element carbon is in its standard
state when it exits as graphite - not as diamond - at 25oC.
Diamond is also a form of carbon, but it is actually slightly less stable
than graphite.
The quantities that we'll use from now on to
compute values for Ho are called the standard enthalpies of
formation of standard heats of formation. The standard heats of formation
of a compound Hfo is the amount of heat absorbed
or evolved when one mole of the compound is formed from its elements in
their standard states. Thus, the thermochemical equation for the formation
of one mole of liquid water from oxygen and hydrogen in their standard
states is
H2(g) + ½O2(g)
H2O(l)
Hfo = -285.8 kJ/mol
The standard enthalpy change for this reaction, that is, the enthalpy
change at 25oC and 1 atm, is called the standard heat of formation
of liquid water. This is a point that often causes confusion among students.
Each of the following equations, for example involves the formation of
CO(g)
C(s) + O2(g)
CO2(g)
CO(g) + ½O2(g)
CO2(g)
2 C(s) + 2 O2(g)
2 CO2(g)
However, only the first involves just the elements
as reactants and the formation of just one mole of CO2. In the
second equation, one of the reactants is a compound, carbon monoxide, and
in the third, two moles of CO2 are formed. Only the first equation,
therefore, has a standard enthalpy change that we identify as Hfo.
Standard heats of formation have been calculated and tabulated. Note
that the Hfo for any element in its standard state
is zero. (0 kJ/mol). This makes sense if you think about it. There
would be no enthalpy change if you "form an element in its standard state
from itself."
The Ho for any reaction must be the difference
between the total enthalpies of formation of the products and those of
the reactants. Any reaction can be generalized by the equation aA + bB
+ ..... nN + mM +
..... where a, b, n, m, etc., are the coefficients of substances A, B,
N, M, etc. The value of Ho can be found using Hess's law equation.
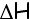o = [nHfo(N)
+ mHfo(M) + ...] - [aHfo(A)
+ bHfo(B) + ...]
Putting this into a more useful form we get:
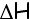o = [sum of the
Hfo of products]-[sum of the Hfo
of reactants]
Consider the following example: Some
chefs keep baking soda, NaHCO3, handy to put out grease fires.
When thrown on the fire, baking soda partly smothers the fire, and the
heat decomposes it to give CO2, which further smothers the flame.
The equation for the decomposition of NaHCO3 is 2 NaHCO3(s)
Na2CO3(s) + H2O(g) + CO2(g).
Calculate
the 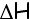o for this
reaction in kilojoules.
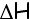o = sum of products
- sum of reactants
= [ Na2CO3(s)
+ H2O(g) + CO2(g)) ] - [ (2)NaHCO3(s)]
Look up the values in the databook tables for each
substance. Make sure the physical states are identical.
= [-1130.7 -241.8 -393.5 kJ/mol ]-[(2)(-950.8 kJ/mol)]
= -1766 kJ/mol - (-1901.6 kJ/mol)
= +135.6 kJ/mol
Under standard conditions, the reaction is endothermic
by 135.6 kJ/mol.
Note that any Ho can be calculated using 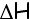o
using
either the reactions or the summation equation. You would just leave
one of the values in the 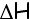o
equation
as unknown and solve the equation.
There
are numerous forms of energy we could investigate. All forms of energy
can be converted to other forms, but within a closed system no energy is
every created or lost. The size of this system depends upon one's
relative view. A beaker could be the system in which case the classroom
would be outside the system and so heat could be lost from the system making
it seem as energy was lost, but we know that in reality it was just lost
to the surroundings. If we consider the entire classroom the system,
then no energy was in fact lost, but only transferred. Thus the law
of conservation of energy holds true even when it does not appear to.
In fact if we consider the system to be to the entire universe, then the
law is never broken. We we consider reactions we must consider both
the system and the surroundings. In chemical reactions only two forms
of energy are consistently prevalent although others appear from time to
time. These ubiquitous forms are kinetic and potential energy.
Kinetic energy is the energy of motion. An object which has motion - whether
it be vertical or horizontal motion - has kinetic energy. There are many
forms of kinetic energy. Recall from quantum chemistry that electrons
are constantly in motion in a variety of ways (orbiting the nucleus, moving
to new levels, spinning and etcetera) and thus represent kinetic energy.
If more kinetic energy is given to an object, some of this energy will
be transferred to increased electron motion. This form of kinetic
energy is therefore always present and always affected by energy changes.
However, its impact is largely limited to the sub-subatomic level (aren't
you glad).
mc2.
The amount of missing mass is known as the mass defect.
